Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài giải:
Tứ giác BCDE có:
BC // DE (vì cùng vuông góc với CD)
BC = DE
nên BCDE là hình chữ nhật
Do đó 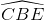 = 900 ,
= 900 , 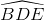 = 900
= 900
Suy ra AB và EF cùng nằm trên một đường thẳn

Xét tứ giác BEDC có:
BC // ED (vì cùng ⊥⊥ CD)
BC = ED (gt)
Nên BEDC là hình bình hành.
Hình bình hành BEDC có \(\widehat{C}=90^o\) nên BEDC là hình chữ nhật.
\(\Rightarrow\widehat{CBE}=\widehat{BED}=90^o\)
Khi đó \(\widehat{ABC}+\widehat{CBE}=180^o\) \(\Rightarrow\) A, B, E thẳng hàng.
\(\widehat{BED}+\widehat{DEF}=180^o\Rightarrow\) B, E, F thẳng hàng.
Vậy AB và EF cùng nằm trên một đường thẳng.

a: Xét tứ giác AEDF có
\(\widehat{AED}=\widehat{AFD}=\widehat{FAE}=90^0\)
Do đó: AEDF là hình chữ nhật
b: Ta có: ΔABC vuông tại A
mà AD là đường trung tuyến
nên AD=BC/2=5(cm)
mà AD=EF(AEDF là hình chữ nhật)
nên EF=5cm
c: Để AEDF là hình vuông thì AD là tia phân giác của góc FAE
=>AD là tia phân giác của góc BAC
Vậy: Khi D là chân đường phân giác kẻ A xuống BC thì AEDF là hình vuông
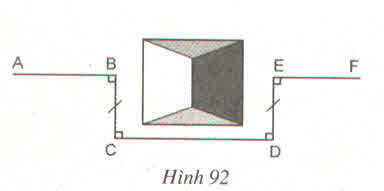
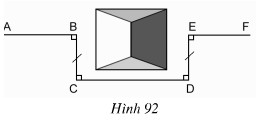
Tứ giác BCDE có:
BC // DE (vì cùng vuông góc với CD);
BC = DE
nên BCDE là hình bình hành ⇒ CD // BE.
Lại có :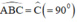 ⇒ AB // CD
⇒ AB // CD
Theo tiên đề Ơ-clit suy ra A, B, E, F thẳng hàng.