Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Độ lêch pha giữa u và i là: \(\Delta \varphi = \varphi_u - \varphi_i = \frac{\pi}{6} - \frac{-\pi}{3} = \frac{\pi}{2}.\)
=> u sớm pha hơn i một góc \(\pi/2\) tức là mạch AB chứa cuộn dây thuần cảm. Còn các trường hợp khác thì không có u sớm pha hơn i một góc 90 độ.
Chọn đáp án. A.
Ta có:
\(U_C=56V\)
\(U_d^2=U_R^2+U_L^2=160^2\) (1)
\(U^2=U_R^2+(U_L-U_C)^2=120^2\)
\(\Rightarrow U_R^2+U_L^2-2U_LU_C+U_C^2=120^2\)
\(\Rightarrow 160^2-2U_L.56+56^2=120^2\)
\(\Rightarrow U_L=128V\)
Thế vào (1) suy ra \(U_R=96V\)
Có \(Z_L=\omega.L=10\pi(\Omega)\)
Có \( \dfrac{U_L}{U_R}=\dfrac{Z_L}{R}\) \(\Rightarrow \dfrac{128}{96}=\dfrac{10\pi}{R}\) \(\Rightarrow R= 7,5\pi(\Omega)\)
Đáp án D
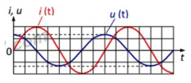
Dựa vào đồ thị ta thấy tại một thời điểm bất kì u luôn nhanh pha hơn i một góc π/2 nên chứng tỏ đoạn mạch chỉ chứa cuộn dây thuần cảm.
Đáp án C.
Nhìn vào mạch điện ta có thể nhận thấy khi cường độ dòng điện có li độ i = ±I0 thì diện áp hiệu dụng hai đầu đoạn mạch là 0. Chứng tỏ điện áp và cường độ dòng điện vuông pha với nhau. Mặt khác lại có:
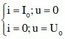nên đoạn mạch này chứa cuộn dây thuần cảm.
Chọn đáp án C
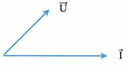
Từ biểu thức u và i ta có 
Vậy u nhanh pha hơn i góc π /3 => giản đồ có dạng như hình bên.
Vậy U → phải được tổng hợp từ U R và U L —› mạch chứa cuộn dây không thuần cảm.
\(U_{RC}=const=U\) khi \(Z_{L1}=2Z_C=R\)
Mặt khác L thay đổi để : \(U_{Lmax}:U_{Lmax}=\frac{U\sqrt{R^2+Z^2_C}}{R}=\frac{U\sqrt{2^2+1}}{2}=\frac{U\sqrt{5}}{2}\)
\(\Rightarrow chọn.D\)
+,có C=C1=>U_R=\frac{U.R}{\sqrt{R^2+(Zl-ZC1)^2}}
+,U R ko đổi =>Zl=ZC1
+,có c=C1/2=>ZC=2ZC1
=>U(AN)=U(RL)=\frac{U\sqrt{r^2+Z^2l}}{\sqrt{R^2+(Zl-2Z^2C1)}}=u=200V
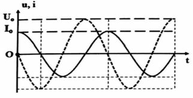
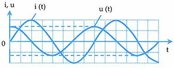
Chọn A
t = 0;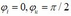
u nhanh pha hơn i một góc vuông. Do đó, mạch này chứa cuộn dây thuần cảm