Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tg ABO \(\sim\Delta A'B'O\)
\(\dfrac{AB}{A'B'}=\dfrac{AO}{A'O}\)=>A'O \(=\dfrac{A'B'.AO}{AB}\)=\(\dfrac{3.2}{1,2}\)=5 (m)(1)
Vậy ảnh cách tk 1 khoảng bằng 5m
Xét tam giác OIF' đồng dạng vs tg A'B'F'
\(\dfrac{OI}{A'B'}=\dfrac{OF'}{A'F'}\)=\(\dfrac{OF'}{A'O-OF'}\)
mà OI = AB = 1,2 m nên
\(\dfrac{AB}{A'B'}=\dfrac{OF'}{A'O-OF'}\)(2)
Từ (1) và (2) suy ra \(\dfrac{AO}{A'O}\)=\(\dfrac{OF'}{A'O-OF'}\)
=>AO(A'O-OF')=OF'. AO
=> 2.(5-OF')=OF'.2
=> 10 -2OF'=2OF'
=> OF'=2,5 (m)
Vậy tiêu cự của TK là 2,5m
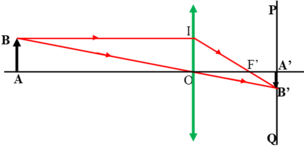
+ Từ B vẽ tia tới đi qua quang tâm O cho tia ló tiếp tục truyền thẳng
+ Từ B vẽ tia tới song song vs trục chính cho tia ló đi qua tiêu điểm F'
+ Tia ló thứ nhất và tia ló thứ 2 giao nhau tại một điểm thì điểm đó là B'
+ Từ B' hạ vuông góc xuống trục chính ta đc A'


Tóm tắt:
AB = 140cm
OA = 2,1m = 210cm
A'B' = 2,8cm
OA'=?
OF' =?
a) \(\Delta ABO\sim\Delta A'B'O\)
\(\Rightarrow\dfrac{AB}{A'B'}=\dfrac{AO}{A'O}\Rightarrow A'O=\dfrac{A'B'}{AB}.OA=\dfrac{2,8}{140}.210=4,2cm\)
b) \(\Delta IF'O\sim\Delta B'F'A'\)
\(\Rightarrow\dfrac{OF'}{A'F'}=\dfrac{OI}{A'B'}\Leftrightarrow\dfrac{OF'}{OA'-OF'}=\dfrac{AB}{A'B'}\Leftrightarrow\dfrac{OF'}{4,2-OF'}=\dfrac{140}{2,8}\)
\(\Rightarrow OF'=\dfrac{140.\left(4,2-OF'\right)}{2,8}=210-OF'\Rightarrow2OF'=210\)
=> OF' = 105cm

Ta có:
h=1,5m
d=6m
d′=4cm=0,04m
Lại có:
h h ' = d d ' → h ' = d ' d h = 0 , 04 6 . 1 , 5 = 0 , 01 m = 1 c m
Đáp án: A

Ta có ΔABO ~ ΔA’B’O nên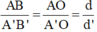
→ Khoảng cách từ ảnh đến vật kính là: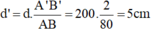

Ảnh ảo, cùng chiều và nhỏ hơn vật.
Khoảng cách từ ảnh đến thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d'}-\dfrac{1}{d}\Rightarrow\dfrac{1}{12}=\dfrac{1}{d'}-\dfrac{1}{9}\Rightarrow d'=\dfrac{36}{7}cm\)
Chiều cao ảnh:
\(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow\dfrac{3}{h'}=\dfrac{9}{\dfrac{36}{7}}\Rightarrow h'=\dfrac{12}{7}cm\)

Ta có:
h=4m
h′=2cm=0,02m
d′=4,5cm=0,045m
Lại có:
h h ' = d d ' → h ' = d ' d h = 4 0 , 02 . 0 , 045 = 9 m
Đáp án: D

a) Dựng ảnh
O A B A' B' F I
b)
Xét các tam giác đồng dạng
IOF với A'B'F \(\Rightarrow \dfrac{IO}{A'B'}=\dfrac{OF}{B'F}\)
ABO với A'B'O \(\Rightarrow \dfrac{IO}{A'B'}=\dfrac{BO}{B'O}\)
Lại có: \(IO=AB\)
Từ đó bạn biến đổi tiếp nhé.