Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+ Trong quá trình dao động của con lắc lò xo treo thẳng đứng.
· Lực phục hồi triệt tiêu tại vị trí cân bằng.
· Lực đàn hồi bị triệt tiêu tại vị trí lò xo không biến dạng.
+ Từ hình vẽ ta có Δt1 = 0,25T và

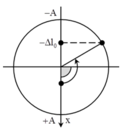
Đáp án A

Kéo vật từ vị trí cân bằng xuống dưới 3cm thì thả vật ra => \(A = 3cm.\)
Hòn bi thực hiện 50 dao động toàn phần trong 20 s
=> Thời gian thực hiện 1 dao động toàn phần (chính là chu kỳ T) : \(T = \frac{20}{50} = 0,4 s.\)
\(\Delta l\) là độ dãn của lò xo khi ở vị trí cân bằng. Tại vị trí cân bằng: \(P = F_{đh}\)
=> \(mg = k\Delta l=> T = 2\pi \sqrt{\frac{m}{k}} = 2\pi\sqrt{\frac{\Delta l}{g}}.\)
=> \(\Delta l = \frac{T^2.g}{4\pi^2} = \frac{T^2}{4} = 0,04 m = 4cm.\)
Lực đàn hồi cực tiểu khác 0 => \(\Delta l \geq A\) => Lực đàn hồi cực tiểu là \(F_{đhmin}=k(\Delta l -A).\)
=> \(\frac{F_{đhmax}}{F_{đhmin}} = \frac{k(\Delta l +A)}{k(\Delta l -A)} = \frac{\Delta l +A}{\Delta l -A} = \frac{4+3}{4-3}= 7.\)

\(T=2\pi\sqrt{\frac{\Delta l_0}{9}}=0,4s\)
\(\Rightarrow\Delta l_0=4=\frac{A\sqrt{2}}{2}\)
Thời gian lò xo không giãn là \(t=2t-\frac{A\sqrt{2}}{2}\Rightarrow-A=\frac{T}{4}=0,10\left(s\right)\)
Vậy D đúng


Lực kéo về triệt tiêu khi đi qua vị trí cân bằng.
Lực đàn hồi triệt tiêu khi đi qua vị trí lò xo k giãn
Tị trí cân bằng cách vị trí lò xo k giãn 1 đoạn là deltal0=mg/k (1)
Từ đường tròn, chia khoảng đi từ biên dưới lên đên vị trí lò xo k giãn làm 4 tức là 1/4 chu kỳ phải bị chia làm 3 xem hình vẽ trên nhé. Khi đó thấy được vị trí lò xo k giãn có li độ -A/2 hay deltal0=A/2 thế vào (1) có được đáp án (để ý T bằng 2 pi căn mờ trên ka)
Giả sử trục tọa độ có gốc ở vị trí cân bằng, chiều dương hướng xuống
Lực đàn hồi triệt tiêu ở vị trí có li độ \(x=-\Delta l_0=-\dfrac{mg}{k}\)
Lực hồi phục triệt tiêu ở gốc tọa độ \(x=0\)
Biểu diễn bằng véc tơ quay, thì để lực hồi phục triệt tiêu véc tơ quay góc \(\alpha = 90^0\)
Suy ra lực hồi phục triệt tiêu thì véc tơ quay một góc là: \(90^0.\dfrac{4}{3}=120^0\)
\(\Rightarrow\dfrac{\Delta l_0}{A}=1/2\)
\(\Rightarrow\dfrac{mg}{kA}=1/2\)
\(\Rightarrow k/m\)
\(\Rightarrow T\)

Bài này có vẻ lẻ quá bạn.
\(W_t=4W_đ\Rightarrow W_đ=\dfrac{W_t}{4}\)
Cơ năng: \(W=W_đ+W_t=W_t+\dfrac{W_t}{4}=\dfrac{5}{4}W_t\)
\(\Rightarrow \dfrac{1}{2}kA^2=\dfrac{5}{4}.\dfrac{1}{2}kx^2\)
\(\Rightarrow x = \pm\dfrac{2}{\sqrt 5}A\)
M N O α α
Thời gian nhỏ nhất ứng với véc tơ quay từ M đến N.
\(\cos\alpha=\dfrac{2}{\sqrt 5}\)\(\Rightarrow \alpha =26,6^0\)
Thời gian nhỏ nhất là: \(\Delta t=\dfrac{26,6\times 2}{360}.T=\dfrac{26,6\times 2}{360}.\dfrac{2\pi}{20}=0.046s\)

\(\Delta l=5cm\)
Vị trí có lực đẩy đàn hồi lần thứ nhất chính là vị trí lò xo bắt đầu bị nén. Tức là qua vị trí -\(x=-\Delta l\).
M -10 10 N -5 ^
Vị trí ban đầu t = 0 tại M ứng với góc (-90 độ).
Vị trí lực đầy đàn hồi lần thứ nhất tại N x = -5 cm.
=> \(\varphi=\pi+\frac{\pi}{6}=\frac{7\pi}{6}\Rightarrow t=\frac{\varphi}{\omega}=\frac{7\pi}{6.10\pi}=\frac{7}{60}s.\)
sai rồi bạn ơi, lực đẩy max là lúc vật ở vị trí -A nhé, denta phi sẽ là 3π/2, và t sẽ là 3/20s

Ta có: \(\begin{cases}\Delta l_1=l_1-l_0=\frac{g}{\omega^2_1}\\\Delta l_2=l_2-l_0=\frac{g}{\omega^2_2}\end{cases}\)\(\Rightarrow\frac{\omega^2_2}{\omega^2_1}=\frac{21-l_0}{21,5-l_0}=\frac{1}{1,5}\)\(\Rightarrow l_0=20\left(cm\right)\)
\(\Rightarrow\Delta l_1=0,01\left(m\right)=\frac{g}{\omega^2_1}\Rightarrow\omega_1=10\pi\left(rad/s\right)\)
KQ = 3,2 cm

Chọn D
+ Từ vị trí cân bằng kéo vật xuống phía dưới để lò xo giãn 10cm rồi thả nhẹ => A = 10cm.
+ Lực phục hồi triệt tiêu tại vị trí cân bằng Δt1 = T/4
+ Lực đàn hồi triệt tiêu khi vật qua vị trí lò xo không giãn:
Vậy chu kì dao động của con lắc là: