Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Phương pháp: Sử dụng lí thuyết về lực kéo về trong dao động điều hòa, dùng đường tròn để tính thời gian trong dao động điều hòa
Cách giải:
Ở vị trí cân bằng lò xo dãn một đoạn ∆l = mg/k = 0,04m = 4cm
Kéo đến khi lò xo dãn 8cm rồi thả nhẹ, vậy biên độ dao động A = 4cm.
Vậy trong quá trình dao động của vật lò xo bị dãn => lực đàn hồi tác dụng lên giá treo luôn có hướng xuống dưới.
Thời điểm có lực đàn hồi tác dụng lên giá treo cùng chiều lực kéo về, vật ở trong khoảng từ VTCB đến biên trên, khoảng thời gian đó là T 2 = π m k = 0 , 2 s

Đáp án D
Phương pháp: Sử dung̣ đường tròn lương̣ giác
Lực hồi phục có chiều luôn hướng về VTCB
Lực đàn hổi sinh ra khi lò xo bị biến dạng và có xu hướng đưa lò xo về trạng thái không biến dạng
Cách giải:
Tần số góc:
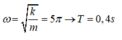
Độ dãn của lò xo ở VTCB: ∆ l = m g k = 4 cm
Kéo vật thẳng đứng xuống dưới để lò xo dãn 12cm rồi thả nhẹ cho vật dao động điều hoà => Biên độ dao động: A = 12 – 4 = 8cm
Biểu diễn trên đường tròn lượng giác khoảng thời gian hai lực cùng chiều (mô tả bởi phần trắng trên đường tròn)
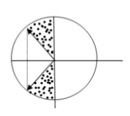
Từ đường tròn lượng giác => t = 5T/6 = 1/3 (s)

Đáp án C.
Theo định luật Húc, ta có độ biến dạng của lò xo tại vị trí cân bằng △ l 0 = m g k
Thay số ta có △ l 0 = 4 (cm)
Biên độ dao động A = Δ l − Δ l 0 = 8 (cm)
Lò xo bị nén từ li độ x = A 2 ta có khoảng thời gian nén Δ t = 2. T 6 = T 3

Đáp án C
Theo định luật Húc, ta có độ biến dạng của lò xo tại vị trí cân bằng D l 0 = m g k
Thay số ta có D l 0 = 4 (cm)
Biên độ dao động A = D l - D l 0 = 8 (cm)
Lò xo bị nén từ li độ x = A 2 ta có khoảng thời gian nén D t = 2 T 6 = T 3

Đáp án A
Ta có ∆l = mg/k = 0,025 m = 2,5 cm.
![]()
![]()
![]()
→ quãng thời gian ![]() ngược chiều nhau là T/6 →
ngược chiều nhau là T/6 →
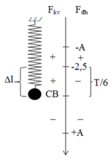 vật
vật
đi từ vị trí π/2 đến 2π/3 và -2π/3 đến –π/2.
→ -A/2 = 2,5 cm.
→ A = 5 cm.

Độ dãn của lò xo khi vật ở VTCB là: \(\Delta \ell_0=\dfrac{mg}{k}=0,04m=4cm\)
Biên độ của vật là: \(A=12-4=8(cm)\)
Chọn trục toạ độ có gốc ở VTCB, chiều dương hướng xuống.
Khi đó, lò xo bị nén thì \(x<-4cm\)
Ta có véc tơ quay
8 x -8 -4 M N O
Trong 1 chu kì, lò xo nén ứng với véc tơ quay từ M đến N
Góc quay \(\alpha = 120^0\)
Thời gian: \(t=\dfrac{120}{360}T=T/3\)
Mà \(T=2\pi\sqrt{\dfrac{m}{k}}=2\pi\sqrt{\dfrac{0,2}{50}}=0,4(s)\)
Độ dãn của lò xo ở vị trí cân bằng là \(\Delta l=\frac{mg}{k}=\frac{0,2.10}{50}=0.04m=4cm.\)
Lò xo dãn tổng cộng 12 cm tức là vị trí của vật là ở li độ: \(x=12-4=8cm.\)
Tại vị trí này thả vật ra không vận tốc đầu tức là biên độ A = 8cm.
Thời gian bị nén trong một chu kì ứng với vị trí cung như đường tròn sau
4cm -8cm 8cm 0 -4cm -A -Delta l A A -A 0 -Delta l M N
Thời gian lò xo bị nén ứng với cung M(-A)N:
\(\cos\varphi_1=\frac{4}{8}=\frac{1}{2}\Rightarrow\varphi_1=\frac{\pi}{3}.\)
\(t=\frac{\varphi}{\omega}=\frac{\frac{2.\pi}{3}}{\sqrt{250}}=\frac{2}{15}s.\)
Như vậy là thời gian bị nén là 2/15 s.

Chọn đáp án A
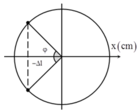
Vì lò xo treo thẳng đứng và có thời gian bị nén nên A > Dl.
Thời gian lực kéo về ngược chiều với lực đàn hồi ứng với vật dao động từ vị trí cân bằng đến vị trí lò xo không biến dạng (tại A) và từ B về VTCB.
→t = 2/15 = (2.(90⁰-j))/ꞷ (1)
Thời gian lò xo bị nén ứng với vật dao động từ A đến B.
→t = 2/15 = 2j/ꞷ (2)
Từ (1) và (2) ® j = 300 ® w = 5p rad/s ® T = 0,4 s
w = g ∆ l = 5p → ∆ l = 0,04m = 4cm
cosj = ∆ l /A→A= ∆ l /cosj = 4/cos30⁰ = 8/ 3 cm

- Vì lò xo treo thẳng đứng và có thời gian bị nén nên A > Δl.
- Thời gian lực kéo về ngược chiều với lực đàn hồi ứng với vật dao động từ vị trí cân bằng đến vị trí lò xo không biến dạng (tại A) và từ B về VTCB.
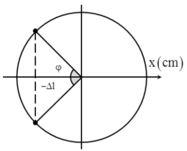
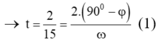
Thời gian lò xo bị nén ứng với vật dao động từ A đến B:
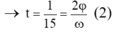
- Từ (1) và (2):


Đáp án A
+ Vì lò xo treo thẳng đứng và có thời gian bị nén nên A > Dl.
+ Thời gian lực kéo về ngược chiều với lực đàn hồi ứng với vật dao động từ vị trí cân bằng đến vị trí lò xo không biến dạng (tại A) và từ B về VTCB.
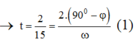
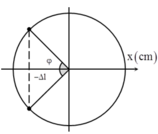
+ Thời gian lò xo bị nén ứng với vật dao động từ A đến B.
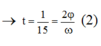
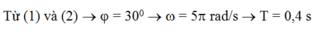
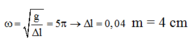
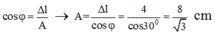
Lực đàn hồi tác dụng lên giá treo ngược chiều với lực đàn hồi tác dụng lên vật.
Nên bài toán trở thành tính thời gian lực đàn hồi tác dụng lên vật ngược chiều với lực hồi phục.
Ở VTCB lò xo giãn: 0,1.10/40 = 0,025m = 2,5cm.
Như vậy, biên độ dao động là: A = 7,5 - 2,5 = 5cm.
5 -5 -2,5 O 30 30
Lực đàn hồi ngược chiều với lực hồi phục ứng với phần gạch đỏ.
Thời gian: \(\frac{60}{360}T=\frac{1}{6}2\pi\sqrt{\frac{0,1}{40}}=\frac{\pi}{60}s\)
Đáp án C.