Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hướng dẫn:
Độ biến dạng của lò xo tại các vị trí cân bằng tạm x 0 = μ m g k = 0 , 01.0 , 2.10 20 = 1 m m
+ Tại vị trí lò xo không biến dạng → so với vị trí cân bằng tạm ở nửa chu kì đầu vật có x 1 = 1 m m .
→ Biên độ dao động trong nửa chu kì đầu là A 1 = x 1 2 + v 1 ω 2 = 1.10 − 3 2 + 1 10 2 ≈ 10 c m
→ Lực đàn hồi cực đại F d h m a x = k A 1 = 1 , 98 N .
Đáp án C

Hướng dẫn: Chọn đáp án A
Tại vị trí có li độ cực đại lần 1, tốc độ triệt tiêu và cơ năng còn lại:
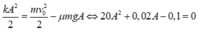
![]()

Chọn D
+ Gọi A là biên độ cực đại của dao động. Khi đó lực đàn hồi cực đại của lò xo trong quá trình dao động Fmax = kA.
+ Để tìm A ta dựa vào định luật bảo toàn năng lượng:
![]()
+ Thay số, lấy g = 10m/s2 ta được phương trình: 0,1 = 10A2 + 0,02A => A = 0,099m (loại nghiệm âm).
+ Do đó Fmax = kA = 1,98N.

Chọn đáp án B.
Do không thay đổi về k, m => ω không đổi.
→ ω = k m = 20 0 , 2 = 10 π ( r a d / s ) .
Ta có năng lượng truyền cho vật là:
E t r u y e n = 1 2 m v 2 = 1 2 .0 , 2.1 2 = 0 , 1 ( J )
⇒ 1 2 k A 2 = E t r u y e n = 0 , 1 ⇒ A = 0 , 1 ( m )
Khi tới biên A lần đầu, năng lượng còn lại là:
![]()
![]()
=> Biên độ còn lại:
![]()

Hướng dẫn: Chọn đáp án A
Tại vị trí lò xo nén cực đại lần 1, tốc độ triệt tiêu và cơ năng còn lại:
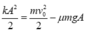
![]()

![]()

Hướng dẫn: Chọn đáp án A
Tại vị trí có li độ cực đại lần 1 tốc độ triệt tiêu và cơ năng còn lại:
![]()
![]()
![]()
![]()
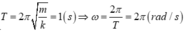
Khi chuyển động từ O đến P thì I’ là tâm dao động nên biên độ là I’P và thời gian
đi từ O đến P tính theo công thức:
![]()
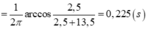
Ta phân tích:
![]()
![]()

Từ điểm này sau thời gian 0,175 (s) vật có li độ so với I là ![]()
![]()
tức là nó có li độ so với O là 1 + 0,454 = 1,454 (cm)

Hướng dẫn:
+ Tốc độ của vật cực đại khi vật đi qua vị trí cân bằng tạm lần đầu tiên
v m a x = ω X 0 − x 0 = k m X 0 − μ m g k = 40 2 c m / s
Đáp án C


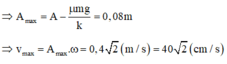
O M x A v
Ban đầu, ở vị trí lò xo không biến dạng, vật ở VTCB O.
Lực đàn hồi đạt giá trị cực đại trong quá trình dao động, chính là vị trí vật ra biên lần đầu tiên, là M(vì ở biên độ tiếp theo thì A giảm dần).
Áp dụng định lý độ giảm cơ năng: \(\Delta W=W_o-W_M=A_{ms}\)
\(W_0=\frac{1}{2}mv^2\)
\(W_M=\frac{1}{2}kA^2\)
\(A_{ms}=\mu mg.A\)
\(\Rightarrow\frac{1}{2}0,2.1^2-\frac{1}{2}20.A^2=0,01.0,2.10.A\)
\(\Rightarrow10A^2+0,02A-0,1=0\)
\(\Rightarrow A=0,099m\)
\(\Rightarrow F_{dh}=k.A=20.0,099=1,98N\)
Đáp án D.