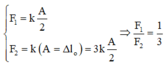Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


T=0.4s => denta l=4 cm
thời gian dãn gấp 2 lần thời gian nén nên tnen = T/3
nếu chọn chiều (+) hướng xuống thì vị trí mà lo xo dãn là từ 2pi/3 -> 4pi/3
nên A = 8 cm

Chọn đáp án C
Theo bài ra trong một chu kì dao động của vật, khoảng thời gian lò xo bị dãn ra là 2 T 3 nên khoảng thời gian lò xo bị nén là T 3 , mà trong một chu kì khoảng thời gian lò xo bị nén chính là khoảng thời gian vật đi từ vị trí lò xo không biến dạng tới biên rồi trở lại vị trí lò xo không biến dạng, tức là vật đi từ A − Δ l o → A → A − Δ l o , theo đó
A − Δ l o = A 2 ⇒ Δ l o = A 2
Từ đây F 1 = k A 2 F 2 = k A + Δ l o = 3 k A 2 ⇒ F 1 F 2 = 1 3

Gọi A là biên độ giao động ta có : kA = 10 N; kA2/2 = 1J => A = 0,2 m = 20 cm
Khoảng thời gian ngắn nhất giữa 2 lần liên tiếp Q chịu tác dụng lực kéo của lò xo có độ lớn \(5\sqrt{3}\)
=> Chu kì giao động của vật T = 0,6s
Quãng đường ngắn nhất đi được là trong 0,4s = \(\frac{2T}{3}\) là s = 3A = 60 cm
Vậy B đúng

Đáp án A
Thời gian lò xo bị nén trong một chu kì là T/3. Lò xo nén khi vật đi từ x = ∆l đến x = A mất t0
→ Trong một chu kì: 2t0 = T/3 → t0 = T/6
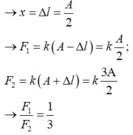

Chọn C
Thời gian lò xo bị nén trong một chu kì là T/3. Lò xo nén khi vật đi từ x = ∆l đến x = A mất t 0
→ Trong một chu kì: 2 t 0 = T/3 → t 0 = T/6
→ x = ∆l = A/2 → F 1 = k(A - ∆l) = k A 2 ; F 2 = k(A + ∆l) = k A 3 → F 1 F 2 = 1 3 .

\(F=\frac{F_{max}\sqrt{3}}{2}\rightarrow t_{min}=\frac{T}{6}=0,1s\rightarrow T=0,6s\)
Từ biểu thức tính năng lượng, tìm được A = 20cm
\(\Delta t=0,4s=\frac{T}{2}+\frac{T}{6}\)
\(\rightarrow S_{max}=2A+A\)
\(S_{max}=60cm\)

Đáp án C.
Theo bài ra trong một chu kì dao động của vật, khoảng thời gian lò xo bị dãn là 2T/3 nên khoảng thời gian lò xo bị nén là T/3, mà trong một chu kì khoảng thời gian lò xo bị nén chính là khoảng thời gian vật đi từ vị trí lò xo không biến dạng tới biên rồi trở lại vị trí lò xo không biến dạng, tức là vật di chuyển đi từ
Từ đây