Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Đổi 4,5o = π/40 rad
Ta có: l = s α = 2 , 5 π π / 40 = 100 c m = 1 m
![]()
![]()

s = α l → l = 1 m → v 2 = g l ( α 0 2 - α 2 ) ≈ 43 cm/s. Chọn D.

Chọn gốc thế năng tại VT dây thẳng đứng.
Áp dụng định luật bảo toàn năng lượng ta có:
\(W=mgl\left(1-\cos\alpha_0\right)=W_d+W_t=W_d+mgl\left(1-\cos\alpha\right)\)
\(\Rightarrow W_d=mgl\left(1-\cos\alpha_0-1+\cos\alpha\right)=mgl\left(\frac{\alpha^2_0}{2}-\frac{\alpha^2}{2}\right)\)
\(=0,1.10.0,8.\left(\frac{\left(\frac{8}{180}\pi\right)^2-\left(\frac{4}{180}\pi\right)^2}{2}\right)\approx5,84\left(mJ\right)\)

\(\omega=\frac{2\pi}{T}=2\pi\)(rad/s)
Vận tốc cực đại \(v_{max}=\omega A=2\pi.5=10\pi\)(cm/s)
Vì vận tốc là đại lượng biến thiên điều hòa theo thời gian, nên ta khảo sát nó bằng véc tơ quay.
10π v 5π M N -10π O
Tại thời điểm t, trạng thái của vận tốc ứng với véc tơ OM, sau 1/6 s = 1/6 T, véc tơ quay: 1/6.360 = 600
Khi đó, trạng thái của vận tốc ứng với véc tơ ON --> Vận tốc đạt giá trị cực đại là: \(10\pi\) (cm/s)
Đáp án B.

Ta có: \(v=\omega\sqrt{s^2_0-s^2}=\sqrt{gl\left(\alpha^2_0-a^2_1\right)}\)\(=0,271\left(m\right)=27,1\left(cm\text{/}s\right)\)
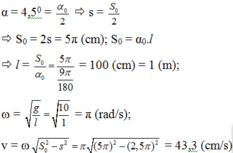

 =2 7,1 cm/s
=2 7,1 cm/s
Chọn đáp án A
Ở thời điểm t 0 , vật nhỏ của con lắc có li độ góc và li độ cong lần lượt là 4 , 5 0 và 2 , 5 π cm.
⇒ α 1 = 4 , 5 0 = 2 π 75 r a d ;
s 1 = 2 , 5 π c m ⇒ l = s 1 α 1 = 93 , 75 c m
⇒ ω = g l = 10 0 , 9375 = 4 6 3 ( r a d / s )
⇒ V max = ω . s 0 = ϖ . l . α 0
= 4 6 3 .0 , 375. 9 180 . π = 6 π 16 m / s
⇒ α 1 α 0 2 + v 1 V max = 2 1
⇒ 1 4 + v 1 V max = 2 1 ⇒ v 1 ≈ 43 c m / s