Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn gốc thế năng tại VT dây thẳng đứng.
Áp dụng định luật bảo toàn năng lượng ta có:
\(W=mgl\left(1-\cos\alpha_0\right)=W_d+W_t=W_d+mgl\left(1-\cos\alpha\right)\)
\(\Rightarrow W_d=mgl\left(1-\cos\alpha_0-1+\cos\alpha\right)=mgl\left(\frac{\alpha^2_0}{2}-\frac{\alpha^2}{2}\right)\)
\(=0,1.10.0,8.\left(\frac{\left(\frac{8}{180}\pi\right)^2-\left(\frac{4}{180}\pi\right)^2}{2}\right)\approx5,84\left(mJ\right)\)

Lực căng dây: \(T=mg(3\cos\alpha-2\cos\alpha_0)\)
Suy ra:
+ Lực căng dây lớn nhất: \(T_{max}=mg(3-2\cos\alpha_0)\) (ở VTCB)
+ Lực căng dây nhỏ nhất: \(T_{min}=mg(3\cos\alpha_0-2\cos\alpha_0)=mg\cos\alpha_0\) (ở biên độ)
Bạn lập tỉ số rồi tìm ra biên đô góc α0

Dùng bảo toàn cơ năng lớp 10! đề không sai !
Với biên độ góc là 600 vẽ hình sẽ thấy độ cao
Nên:

Cái này hình như bạn viết nhầm đơn vị của g phải là m/s2
Khi lò xo có chiều dài l=28 thì vận tốc bằng 0=> vật ở vị trí biên âm
△l=|△l0-A|=2cm
Fd=k|△l|=2N
=>k=100N/m
△l0=\(\dfrac{m.g}{k}\)=0,02(m)=2cm
=>A=4cm
W=1/2.k.A2=0,08j

Ta có: \(v=\omega\sqrt{s^2_0-s^2}=\sqrt{gl\left(\alpha^2_0-a^2_1\right)}\)\(=0,271\left(m\right)=27,1\left(cm\text{/}s\right)\)

Chu kì riêng của con lắc: \(T=2\pi\sqrt{\frac{l}{g}}=2,8s\)
Vậy khi chu kì của ngoại lực tăng từ 2s đến 4s thì biên độ ̣con lắc tăng rồi giảm
Đáp án D

Do E và B biến thiên cùng pha nên, khi cảm ứng từ có độ lớn B0/2 thì điện trường E cũng có độ lớn E0/2.
Bài toán trở thành tính thời gian ngắn nhất để cường độ điện trường có độ lớn E0/2 đang tăng đến độ lớn E0/2.
E M N Eo Eo/2
Từ giản đồ véc tơ quay ta dễ dang tính được thời gian đó là t = T/3
Suy ra: \(t=\dfrac{5}{3}.10^{-7}\)s

\(W_t=W_0-W_d=W_0-W_0sin^2\left(\omega t\right)=W_0cos^2\left(\omega t\right)\\\)
\(\Rightarrow W_{tmax}\Leftrightarrow cos^2\left(\omega t\right)=1\\ \Rightarrow W_{tmax}=W_0\)

Sử sụng hệ thức: 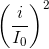 +
+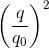 = 1
= 1
Thay số và giải hệ phương trình trìm I0 và q0
Tần số góc: ω = 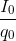 = 50 (rad/s)
= 50 (rad/s)

 =2 7,1 cm/s
=2 7,1 cm/s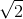
Chọn B
+ Lực căng dây: T = mg(3cosα – 2cosαo)
=> Tmax = mg(3 - 2cosαo)
Tmin = mgcosαo
+ Ta có: Tmax = 1,02 Tmin ⇔ 3 - 2cosαo = 1,02cosαo => αo ≈ 0,1149 rad ≈ 6,6o.