Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Gia tốc biểu kiến của con lắc nằm trong thang máy chuyển động với gia tốc \(\overrightarrow a\) là:
\(\overrightarrow {g'} = \overrightarrow {g} -\overrightarrow a \)
Thang máy đi lên chậm dần đều nên \(\overrightarrow g \uparrow \uparrow \overrightarrow a\) => \( {g'} ={g} -a \)
Mà \(a = \frac{g}{2} => g' = g - \frac{g}{2} = \frac{g}{2}.\)
Chu kì của con lắc lúc này là \(T' =2\pi \sqrt{\frac{l}{g}} = 2\pi \sqrt{\frac{2l}{g}} = T\sqrt{2}.\)
Chọn C
+Trong hệ quy chiếu chuyển động với gia tốc 
, vật nặng có giá tốc trọng trường biểu kiến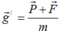 
Do lực lạ (lực quán tính) 
a hướng lên à g/ = g + a
a hướng xuống à g/ = g - a
+ Trong trường hợp cụ thể à
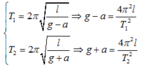
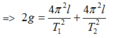
+ Thay số được T = 2,78s.
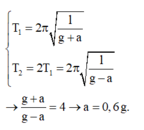
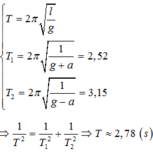
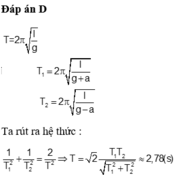
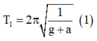
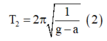
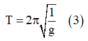
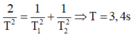
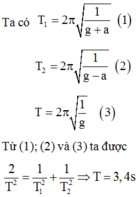
Đáp án C
Phương pháp: Sử dụng lí thuyết về bài toán con lắc đơn chịu tác dụng của lực quán tính
Cách giải:
+ Khi thang máy đi lên NDĐ với gia tốc có độ lớn là a thì gia tốc trọng trường hiệu dụng : g1 = g + a
=> Chu kì dao động: T 1 = 2 π l g + a
+ Khi thang máy đi lên CDĐ với gia tốc có độ lớn là a thì gia tốc trọng trường hiệu dụng : g2 = g – a
=> Chu kì dao động T 2 = 2 π l g - a
+ Theo đề bài T 2 = 2 T 1 ⇒ π l g - a = 2 l g + a => g + a = 4(g-a) => a = 3g/5
=> Chọn C