Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

T=1s.
Trong thời gian 0,5s = T/2 vật đi quãng đường là 2.A = 2.8=16cm.

Phương trình tổng quát: \(x= A cos(\omega t+\varphi)\)
+ Tần số góc: \(\omega = 2\pi/2 = \pi \ (rad/s)\)
+ t=0, vật qua VTCB theo chiều đương \(\Rightarrow\left\{ \begin{array}{} x_0 = 0\ cm\\ v_0 >0 \end{array} \right.\)\(\Rightarrow\left\{ \begin{array}{} \cos \varphi = 0\ cm\\ \sin \varphi <0 \end{array} \right. \Rightarrow \varphi = -\frac{\pi}{2}\)
Vậy phương trình dao động: \(x = 5\cos(\pi t - \frac{\pi}{2})\) (cm)
tại sao lại ra φ=\(\dfrac{-\pi}{2}\) làm cách nào vậy bạn???

Đáp án C
(a) Chu kì của dao động là T = 2 π ω = 2 s → ( a ) s a i
(b) Tốc độ cực đại của chất điểm là v m a x = ω . A = 18 , 8 c m / s → ( b ) đ ú n g
(c) Gia tốc của chất điểm có độ lớn cực đại là a m a x = ω 2 A = 59 , 2 c m / s 2 → ( c ) sai
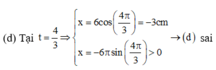
(e) Tốc độ trung bình của vật trong một chu kì dao động là v t b = 4 A T = 12 c m / s → ( e ) đ ú n g
(f) Tốc độ trung bình của vật trong một nửa chu kì dao động là v t b = 2 A 0 , 5 T = 12 c m / s → (f) sai
(g) Trong 0,25T vật có thể đi được quãng đường
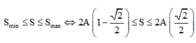
![]()

Lần lượt kiểm tra từng phương án, ta thấy phương án đúng là \(v_{max} = \omega A = 6.\pi = 18,8 \ cm\)

Lần lượt kiểm tra từng phương án, ta thấy phương án đúng là \(v_{max} = \omega A = 6.\pi = 18,8 \ cm\)

Góc mà vật quay được là \(\varphi = t\omega = 0.157.10 = 1,57 (rad) = 0.5\pi. (rad)\)
-π/3 M N a π/6 A/2
Như vậy quãng đường đi được là hình chiếu của cung \(MaN\) tương ứng trên trục 0x nằm ngang tức là
\(S = (A- \frac{A}{2})+(A- \frac{A\sqrt{3}}{2}) = A (2-\frac{1}{2} - \frac{\sqrt{3}}{2}) = 1,9cm.\)
chon D.

Tốc độ góc của chuyển động: \(\omega = 10\pi (rad/s)\)
Bán kính quỹ đạo: R = 6cm.
Tốc độ chuyển động (tốc độ dài): \(v = \omega R = 10\pi .6 = 60\pi (cm/s)\)



v=\(\frac{2A}{\frac{T}{2}}\)=2A\(\omega\)/\(\pi\)= 2*4*4\(\pi\)/\(\pi\)=32
Cảm ơn bạn Hue nhé, mình hơi gà mờ cái này.