Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do gia tốc a vuông pha với vận tốc v, nên ta có: \((\frac{a}{a_{max}})^2+(\frac{v}{v_{max}})^2 =1\) \(\Rightarrow (\frac{a}{\omega^2 A})^2+(\frac{v}{\omega A})^2=1\) \(\Rightarrow \frac{v^2}{\omega ^2}+\frac{a^2}{\omega ^4} = A^2\)

Đáp án D
+ Với hai đại lượng vuông pha, ta có:
v ωA 2 + a ω 2 A 2 = 1 → m v 2 A 2 + m 2 a 2 A 2 = 1 → A 2 = m v 2 + ma 2

Phương trình tổng quát: \(x= A\cos(\omega t +\varphi)\)
Áp dụng công thức độc lập: \(A^2 = x^2 +\frac{v^2}{\omega ^2} \Rightarrow (\frac{x}{A})^2+(\frac{v}{\omega A})^2=1\)\(\Rightarrow\left\{ \begin{array}{} A^2 = 16\ \\ \omega^2 A^2 =640 \end{array} \right.\)\(\Rightarrow\left\{ \begin{array}{} A = 4\ \\ \omega =2\pi \end{array} \right.\)
t = 0\(\Rightarrow\left\{ \begin{array}{} x_0 = A/2\\ v_0 <0 \end{array} \right.\)\(\Rightarrow\left\{ \begin{array}{} \cos \varphi = \frac{1}{2}=0,5\\ \sin \varphi >0 \end{array} \right. \Rightarrow \varphi = \frac{\pi}{3}\)
Phương trình dao động: \(x=4\cos(2\pi t +\frac{\pi}{3}) \ (cm)\)

Bài 3:
Lại đạo hàm :<
Have: \(\left(\frac{x}{v}\right)'=\frac{x'v-v'x}{v^2}\)
Have also: \(\left\{{}\begin{matrix}v=x'\\v'=a=-\omega^2x\end{matrix}\right.\)
\(\Rightarrow\left(\frac{x}{v}\right)'=\frac{v^2+\omega^2x^2}{v^2}=1+\frac{x^2}{\frac{v^2}{\omega^2}}=1+\frac{x^2}{A^2-x^2}\)
Đạo hàm 2 vế theo thời gian biểu thức: \(\frac{x_1}{v_1}+\frac{x_2}{v_2}=\frac{x_3}{v_3}\) :
\(\left(1+\frac{x_1^2}{A_1^2-x_1^2}\right)+\left(1+\frac{x_2^2}{A_2^2-x_2^2}\right)=1+\frac{x_3^2}{A_3^2-x_3^2}\)
\(\Rightarrow1+\frac{x_1^2}{A_1^2-x_1^2}+\frac{x_2^2}{A_2^2-x_2^2}=\frac{x_3^2}{A_3^2-x_3^2}\Rightarrow\left|x_3\right|=3,4\left(cm\right)\)
Bài 2:
\(Cauchy:A_1+A_2\ge2\sqrt{A_1A_2}\Leftrightarrow10\ge2\sqrt{A_1A_2}\Rightarrow A_1A_2\le25\)
Have: \(A_1A_2=\sqrt{x_1^2+\frac{v_1^2}{\omega^2}}.\sqrt{x_2^2+\frac{v_2^2}{\omega^2}}=\sqrt{\left(x_1^2+\frac{v_1^2}{\omega^2}\right)\left(x_2^2+\frac{v_2^2}{\omega^2}\right)}\)
\(Bunhiacopxki:\left(a_1^2+a_2^2\right)\left(b_1^2+b_2^2\right)\ge\left(a_1b_1+a_2b_2\right)^2\)
\(\Rightarrow\left(x_1^2+\frac{v_1^2}{\omega^2}\right)\left(x_2^2+\frac{v_2^2}{\omega^2}\right)\ge\left(x_1.\frac{v_2}{\omega}+x_2.\frac{v_1}{\omega}\right)^2\)
\(\Rightarrow A_1A_2\ge\left(x_1.\frac{v_2}{\omega}+x_2\frac{v_1}{\omega}\right)\Leftrightarrow25\ge\left(\frac{x_1.v_2+x_2v_1}{\omega}\right)\)
\(\Leftrightarrow x_1v_2+x_2v_1\le25\omega\Leftrightarrow9\le25\omega\)
\(\Rightarrow\omega\ge\frac{9}{25}=0,36\left(rad/s\right)\)
This exercise is hardest :<

Đáp án C
+ Sử dụng công thức độc lập cho hai đại lượng vuông pha
v v max 2 + a a max 2 = 1 ↔ v ω A 2 + a ω 2 A 2 = 1 hay v 2 ω 2 + a 2 ω 4 = A 2
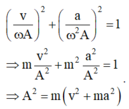
Đáp án D
Với hai đại lượng vuông pha, ta có: