Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sửa đề: Chiều dài từ gốc cây đến chỗ cây bị gãy là 3m
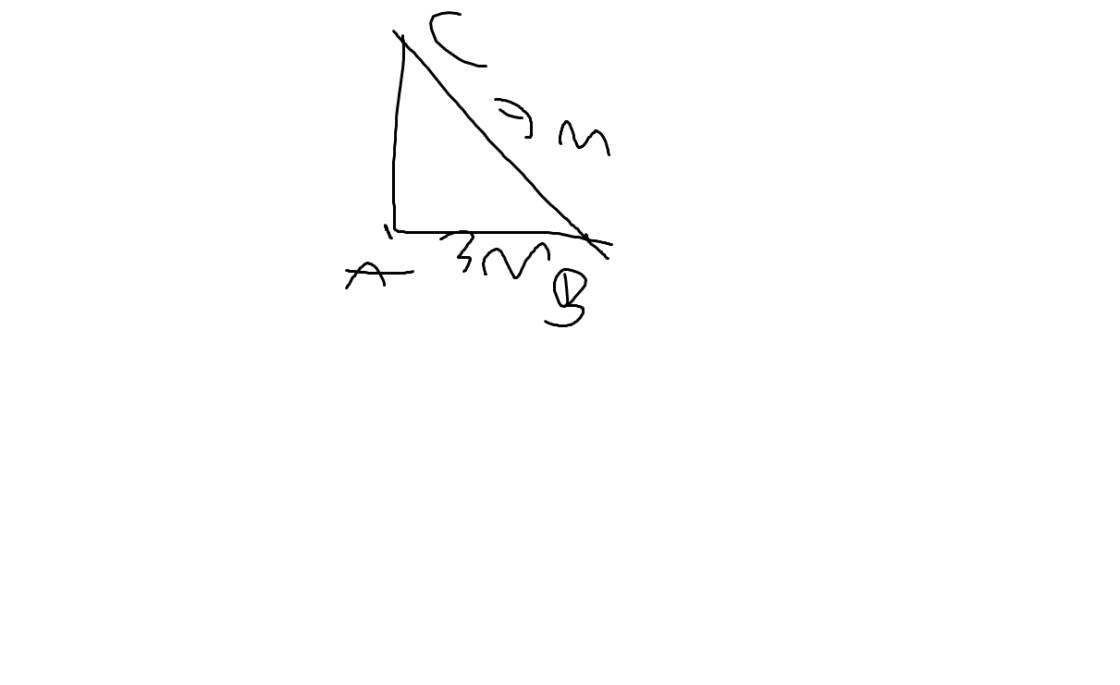
Gọi A là gốc của cái cây
Gọi Clà ngọn của cái cây
Gọi B là chỗ cây bị gãy
Do đó, ta có: \(AB\perp AC\)
Theo đề, ta có: BC=7m; AB=3m
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC=\sqrt{7^2-3^2}=2\sqrt{10}\left(m\right)\simeq6,3\left(m\right)\)

Phần gãy dài \(\sqrt{6^2+8^2}=10(m)\)
Vậy cây cao \(10+6=16(m)\)

Áp dụng đ/l Pytago vào tam giác vuông ABC, có :
\(BC^2=AB^2+AC^2\\ \Rightarrow AC^2=BC^2-AB^2\\ \Rightarrow AC=\sqrt{4^2-3^2}\\ =\sqrt{7}\left(m\right)\)
Chiều cao của cây lúc chưa gãy là :
\(4+\sqrt{7}\approx6,6\left(m\right)\)
A B C 4 3
Áp dụng định lý Pytago cho tam giác ABC ta có:
\(AB^2+AC^2=BC^2\)
Thay số: \(3^2+4^2=BC^2\)
\(BC^2=25 \)
\(BC=5\)
Vậy chiều cao của cái cây lúc chưa bị gãy là:
\(5 +4 = 9m\)

Giải
Giả sử AE là cây cọ cao 30m và BC là cây cọ cao 20m. Nếu gọi khoảng cách từ
gốc E đến con cá D là x (m) thì khoảng cách từ gốc C đến con cá D là: 50 - x (m)
Hai con chim cùng bay một lúc và vồ được cá cùng một lúc nên AD = BD
Theo định lí Pitago ta có:
30\(^2\) + x\(^2\) = 20\(^2\) + (50 – x)\(^2\)
900 + x\(^2\) = 400 + (2500 – 100 . x + x\(^2\))
Từ đó 100 . x = 2000, suy ra x = 20 (m)
Vậy con cá cách gốc cây cọ cao 30m là 20m

Lời giải:
Ký hiệu gốc cây là $A$, ngọn cây bị gãy là $B$, điểm gãy là $C$. Ta có:
$AC+CB=8(1)$ (m)
$AB=4$ (m)
Áp dụng định lý Pitago:
$AC^2+AB^2=BC^2$
$\Rightarrow AC^2+4^2=BC^2$
$\Rightarrow BC^2-AC^2=16$
$\Rightarrow (BC-AC)(BC+AC)=16$
$\Rightarrow (BC-AC).8=16\Rightarrow BC-AC=2(2)$
Từ $(1); (2)\Rightarrow BC=(8+2):2=5; AC=(8-2):2=3$ (m)
Vậy độ dài từ điểm gãy tới gốc là $AC=3$ m
Hình vẽ: