Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: chiều cao của người đó là AB'
Gọi t là thời gian đi B->B'
v là vận tốc chuyển động trong thời gian t thì BB'=v.t
Gọi quãng đường đi B->B'' là x.
Ta có:
\(\Delta AB'B''\) đồng dạng với \(\Delta SBB''\)
\(\Leftrightarrow \dfrac{AB'}{SB} = \dfrac{B'B"}{BB'' }\)
\(\Leftrightarrow \dfrac{h}{H} = \dfrac{B'B"}{x }
\)
\(\Leftrightarrow B'B" = \dfrac{h.x}{H}\)
BB" = BB' + B'B"
\(\Leftrightarrow x = v.t + \dfrac{h.x}{H}\)
\(\Leftrightarrow Hx = H.v.t + h.x\) ( nhân cả 2 vế cho H)
\(\Leftrightarrow Hx - h.x = H.v.t
\)
\(\Leftrightarrow x( H-h) = H.v.t\)
\(\Leftrightarrow x = \dfrac{H.v.t}{h-x}(*)\)
mà \(v' = \dfrac{BB"}{t}\)
Từ (*). Ta có:
\(v' =\dfrac{BB"}{t} = \dfrac{H.v.t}{h-x} : t = \dfrac{H.v}{H-h}\)
Vậy vận tốc chuyển động của bóng của đỉnh đầu là

Chiều cao cột đèn :
\(l=2+\left[cos\left(55\right).20\right]\approx13,47\left(m\right)\)

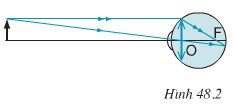
Trên hình ta biểu diễn cột điện bằng đoạn AB (AB = 8 cm); O là thể thủy tinh (OA = 20 m); A'B' là ảnh cột điện trên màng lưới (OA' = 2 cm). Ta có:
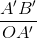 =
= 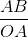 => A'B' =
=> A'B' = 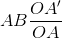 = 0,8 cm
= 0,8 cm

Quá trình tạo ảnh của thể thủy tinh được mô phỏng bằng hình vẽ sau: (coi màn PQ như màng lưới trên võng mạc của mắt).
Ký hiệu cột điện là AB, ảnh của cột điện trên màng lưới là A’B’, thể thủy tinh là thấu kính hội tụ đặt tại O. Ta có: AO = 20m = 2000cm; A’O = 2cm; AB = 8m = 800cm.
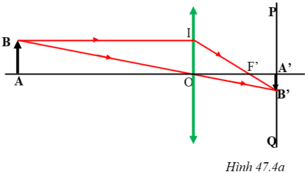
Hai tam giác ABO và A’B’O đồng dạng với nhau, ta có:
![]()
Chiều cao của ảnh cột điện trên màng lưới là:
![]()
giải giúp mìn với đang cần gấp