Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi bán kính của hình cầu là R thì dung tích của bình là
\(V=\frac{4}{3}\pi R^3=1l=10^{-3}m^3\). Suy ra : \(R\approx0,06\)
Diện tích mặt cầu là \(S=4\pi R^2\). Một phân tử khí chiếm diện tích là \(d^2=10^{-20}m^2\)
Số đơn phân tử bám vào thành bình là \(N=\frac{4\pi R^2}{d^2}\). Ở nhiệt độ \(300^oC\), số phân tử ở thành bình sẽ được giải phóng và chiếm toàn bộ dung tích của bình. Vậy mật độ phân tử khí trong bình là :
\(n=\frac{N}{V}=\frac{3}{d^2R}=5.10^{21}m^{-3}\)

Ta có : T1 = toC + 273 = 30 + 273 = 303oK
p1 = 2 bar = 2 . 105 Pa
p2 = 4 bar = 4 . 105
Vì quá trình là đẳng tích , áp dụng định luật Charles ta có
\(\frac{p_1}{p_2}=\frac{T_1}{T_2}\)→ T2 = \(\frac{p_2.T_1}{p_1}=\frac{4.10^5.303}{2.10^5}\)= 606oK
Vậy để áp suất tăng lên gấp đôi , ta phải tăng nhiệt độ lên 606oK
* Trạng thái 1: T1 = 273 + 30 = 303 K
p1 = 2 bar
* Trạng thái 2: T2 = ? p2 = 2p1
* Vì thể tích bình không đổi nên:
\(\frac{P1}{T1}=\frac{P2}{T2}\Rightarrow T2=\frac{P2.T1}{P1}=\frac{2P1.T1}{P1}\) = 2T1 = 606 K

B3: to = 20C
\(\Delta l=l_o\alpha\left(50-20\right)=0,0033m\)
=> phải để hở 1 khe lớn hơn hoặc = 0,0033m
B1: a, \(\Delta l=l_o\alpha\left(40-20\right)=0,00033m\)
b, \(l=\Delta l+l_o=1,50033m\)
B5: Ta co: \(V=V_o\left[1+3\alpha\left(t-t_o\right)\right]\)
=> \(\frac{m}{D}=\frac{m}{D_o}\left[1+3\alpha\left(500-0\right)\right]\)
=> D \(\approx6885,4\)
B2: \(l-l_o=l_o\alpha\left(t-0\right)\)
=> \(l_o\alpha\left(t-0\right)=0,0008\)
=> \(t\approx72,7^oC\)

Tính áp suất p' của khí trong bình .
Lúc đầu khí trong bình (1) có \(\begin{cases}V_1\\p=10^5Pa\\T=300K\end{cases}\) bình (2) có: \(\begin{cases}V_2=2V_1\\p\\T\end{cases}\)
Số mol khí trong hai bình \(n=\frac{3pV_1}{RT}\)
Lúc sau, khí trong bình (1) có \(\begin{cases}V_1\\p'\\T_1=273K\end{cases}\) bình (2) có \(\begin{cases}V_2=2V_1\\p'\\T_2=330K\end{cases}\)
Số mol khí trong bình (1): \(n_1=\frac{p'V_1}{RT_1}\), trong bình (2): \(n_2=\frac{2p'V_1}{RT_2}\)
\(n=n_1+n_2\Leftrightarrow\frac{3pV_1}{RT}=\frac{p'V_1}{RT_1}+\frac{2p'V_2}{RT_2}\)
\(\frac{3p}{T}=p'\left(\frac{1}{T_1}+\frac{2}{T_2}\right)\) suy ra \(p'=1,024.10^5Pa\)
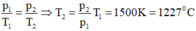
Đáp án C.