Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) chỉ dùng R1 ta có \(Q=k.\dfrac{U^2}{R1}.t1\) (1)
Chỉ dùng R2 => \(Q=k.\dfrac{U^2}{R2}.10\) (2)
Lấy 1:2 => \(1=\dfrac{R2.t1}{10.R1}=>t1=\dfrac{20}{3}phút\)
b) R1ntR2=>Q=\(k.\dfrac{U^2}{R1+R2}.tnt=\dfrac{U^2}{20}.k.tnt\) (3)
Lấy 2:3=>\(1=\dfrac{20.10}{tnt.R2}=>tnt=\dfrac{50}{3}phút\)
c) mắc R1//R2=>\(Q=k.\dfrac{U^2}{\dfrac{8.12}{8+12}}.tss\) (4)
Lấy 2:4=>\(1=\dfrac{10.24}{tss.5.12}=>tss=4\) phút
Vậy.......

\(=>Qtoa1=Qthu1+Qhp1\)
\(=>Qtoa1=mC\Delta t+kt1\)(k: hằng số)
\(=>\dfrac{U1^2}{R}=mC\Delta t+k.t1\left(1\right)\)
tương tự \(=>\dfrac{U2^2}{R}=mC\Delta t+k.t2\left(2\right)\)
\(=>\dfrac{U3^2}{R}=m.C\Delta t+k.t3\left(3\right)\)
lấy (2) trừ (1)\(=>\dfrac{U2^2}{R}-\dfrac{U1^2}{R}=kt2-kt1=k\left(t2-t1\right)\)
\(=>\dfrac{U2^2-U1^2}{R}=k\left(t2-t1\right)\left(4\right)\)
lấy(3) trừ(2)\(=>\dfrac{U3^2-U2^2}{R}=k\left(t3-t2\right)\left(5\right)\)
lấy (5) chia (4) \(=>\dfrac{U3^2-U2^2}{U2^2-U1^2}=\dfrac{t3-t2}{t2-t1}=>U3=.....\)
bạn thay số vào tính U3 nhé
có hệ số k
vì đề cho nhiệt lượng hap phí tỉ lệ thuận với thời gian
\(=>\dfrac{Qhp1}{t1}=\dfrac{Qhp2}{t2}=\dfrac{Qhp3}{t3}\)
nên đặt \(\dfrac{Qhp1}{t1}=\dfrac{Qhp2}{t2}=\dfrac{Qhp3}{t3}=k\)
\(=>Qhp1=kt1,Qhp2=kt2,Qhp3=kt3\)
rồi áp dụng \(Qtoa=Qthu+Qhp=>Qtoa1=mc\Delta+Qhp1=mc\Delta+k.t1\)
do đun nước thì cả 3 trường hợp Qthu như nhau vì cùng khối lượng nước với cùng nhiệt dung riêng với cùng đun sôi nước từ 1 nhiệt độ nào đó lên 100oC nhé

Nhiệt lượng cần cung cấp để đun sôi 1,5 lít nước là:
Q = 420000.1,5 = 630000 J
Theo công thức tính nhiệt lượng tỏa ra của ấm ta có:
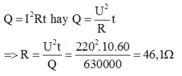
→ Đáp án C

`*` Tóm tắt:
\(R=80\Omega\\ I=2,5A\\ m=1,5l=1,5kg\\ t_0=100^oC\\ t_1=25^oC\\ t=20min=1200s\\ c=4200J/kg\cdot K\\ t_b=3h\\ 1kWh=1700đ\\ ------------\\ a)Q=?J\\ b)T_{30}=?đ\)
_
`*` Giải:
`a)` Nhiệt lượng cần thiết để đun sôi nước:
\(Q=m\cdot c\cdot\left(t_0-t_1\right)=1,5\cdot4200\cdot\left(100-25\right)=472500J\)
`b)` Điện năng sử dụng trong `30` ngày là:
\(A=I^2\cdot R\cdot t=2,5^2\cdot80\cdot\left(3\cdot30\right)=45000Wh=45kWh\)
Tiền điện phải trả cho việc sử dụng bếp điện đó trong `30` ngày là:
\(T=45\cdot1700=76500đ.\)

* Gọi Q (J) là nhiệt lượng mà bếp cần cung cấp cho ấm để đun sôi nước thì Q luôn không đổi trong các trường hợp trên. Nếu ta gọi t1 ; t2 ; t3 và t4 theo thứ tự là thời gian bếp đun sôi nước tương ứng với khi dùng R1, R2 nối tiếp; R1, R2 song song ; chỉ dùng R1 và chỉ dùng R2 thì theo định luật Jun-lenxơ ta có :
\(Q=\frac{U^2.t}{R}=\frac{U^2.t_1}{R_1+R_2}=\frac{U^2.t_2}{\frac{R_1.R_2}{R_1+R_2}}=\frac{U^2.t_3}{R_1}=\frac{U^2.t_4}{R_2}\) (1)
* Ta tính R1 và R2 theo Q; U ; t1 và t2 :
+ Từ (1) \(\Rightarrow\) R1 + R2 = \(R_1+R_2=\frac{U^2t_1}{Q}\)
+ Cũng từ (1) \(\Rightarrow\) R1 . R2 = \(R_1.R_2=\frac{U^2t_2}{Q}\left(R_1+R_2\right)=\frac{U^4t_1t_2}{Q^2}\)
* Theo định lí Vi-et thì R1 và R2 phải là nghiệm số của phương trình :
R2 - \(\frac{U^2t_1}{Q}.R+\frac{U^4t_1t_2}{Q^2}=0\)(1)
Thay t1 = 50 phút ; t2 = 12 phút vào PT (1) và giải ta có \(\Delta=10^2.\frac{U^2}{Q^2}\Rightarrow\sqrt{\Delta}=\frac{10.U^2}{Q}\) .
\(\Rightarrow\) \(R_1=\frac{\frac{U^2t_1}{Q}+\frac{10U^2}{Q}}{2}=\frac{\left(t_1+t_2\right)U^2}{2Q}=30\frac{U^2}{Q}\) và \(R_2=20.\frac{U^2}{Q}\)
* Ta có \(t_3=\frac{Q.R_1}{U^2}\)= 30 phút và \(t_4=\frac{Q.R_2}{U^2}\) = 20 phút . Vậy nếu dùng riêng từng điện trở thì thời gian đun sôi nước trong ấm tương ứng là 30 phút và 20 phút .

Okie iem :3
\(Q=P.t=1000.t\left(J\right)\)
\(Q_{toa}=mc\left(100-20\right)=4.4200.80\left(J\right)\)
Áp dụng phương trinh cân bằng nhiệt:
\(\Rightarrow Q=Q_{toa}\Leftrightarrow1000t=4.4200.80\Rightarrow t=...\left(s\right)\)
b/ Con số 1000 W cho biết công suất của ấm khi hoạt động bình thường
c/ Điện trở được gập làm đôi, nghĩa là cắt dây đó thành 2 phần bằng nhau rồi mắc song song
\(R'=\dfrac{1}{2}R=\dfrac{1}{2}.\dfrac{U^2_{dm}}{P_{dm}}=\dfrac{1}{2}.\dfrac{220^2}{1000}=...\left(\Omega\right)\)
\(\Rightarrow R_{td}=\dfrac{R'}{2}=...\left(\Omega\right)\Rightarrow Q'=\dfrac{U^2_{dm}}{R_{td}}.t\left(J\right)\)
\(\Rightarrow Q'=Q_{toa}\Leftrightarrow\dfrac{220^2}{R_{td}}.t'=4.4200.80\Rightarrow t'=...\left(s\right)\)
