Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn đáp án C
Lượng tia γ phóng xạ lần đầu:
Sau thời gian 2 tháng, một nửa chu kì t = T/2, Lượng phóng xạ trong nguồn phóng xạ sử dụng lần đầu còn:
Thời gian chiếu xạ lần này Δ ∆ t’
→ 
Vì bệnh nhân được chiếu xạ với cùng một lượng tia γ như lần đầu nên Δ ∆ N’ = Δ ∆ N
Do đó 
phút.
Đáp án D
+ Gọi N 0 là số hạt của mẫu phóng xạ ban đầu.
Ban đầu ta có
+ Lần chiếu xạ thứ 4 ứng với thời gian là 3 tháng.
Số hạt của mẫu phóng xạ còn lại là:
+ Để bệnh nhân nhận được lượng tia g như lần đầu tiên thì:
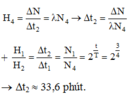
Đáp án D
+ Gọi N 0 là số hạt của mẫu phóng xạ ban đầu.
Ban đầu ta có: 
+ Lần chiếu xạ thứ 4 ứng với thời gian là 3 tháng.
Số hạt của mẫu phóng xạ còn lại là: 
+ Để bệnh nhân nhận được lượng tia g như lần đầu tiên thì:
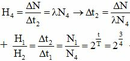
® D t 2 » 33,6 phút.
Đáp án C
Khi x bé ta có: 
Xem lượng tia gamma phát ra tỉ lệ với số nguyên tử bị phân rã.
Số nguyên tử bị phân trong lần chiếu xạ đầu tiên: 
Thời gian chiếu xạ lần thứ ba: 
Mặt khác: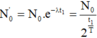 
. Với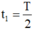 
(là 2 tháng)
Do đó ta có: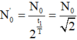 
Từ (1) và (2) ta có: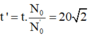 
phút
độ phóng xạ \(\beta^-\) của một tượng gỗ bằng 0,8 lần độ phóng xạ của một khúc gỗ cùng khối lượng lúc mới chặt
Ta có: \(\frac{hc}{\lambda}=A+\frac{1}{2}mv^2_{0max}\left(\text{∗}\right)\)
+Khi chiếu bức xạ có \(\lambda_1:v_{0max1}=\sqrt{\frac{2\left(\frac{hc}{\lambda_1}-A\right)}{m}}\left(1\right)\)
+Khi chiếu bức xạ có \(\lambda_2:v_{0max2}=\sqrt{\frac{2\left(\frac{hc}{\lambda_2}-A\right)}{m}}\left(2\right)\)
Từ \(\text{(∗)}\) ta thấy lhi \(\lambda\) lớn thì \(v_{0max}\) nhỏ
\(\Rightarrow v_{0max1}=2,5v_{0max2}\left(\lambda_1<\lambda_2\right)\)
\(\Leftrightarrow\sqrt{\frac{2\left(\frac{hc}{\lambda_2}-A\right)}{m}}=2,5\sqrt{\frac{2\left(\frac{hc}{\lambda_2}-A\right)}{m}}\)
\(\Leftrightarrow\frac{hc}{\lambda_1}-A=6,25\left(\frac{hc}{\lambda_2}-A\right)\) với \(A=\frac{hc}{\lambda_0}\)
\(\Rightarrow\lambda_0=\frac{5,25\lambda_1\lambda_2}{6,25\lambda_1-\lambda_2}=\frac{5,25.0,4.0,6}{6,25.0,4-0.6}=0,663\mu m\)
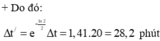
Đáp án C