Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trả lời:
\(\frac{5}{1.6}+\frac{5}{6.11}+...+\frac{5}{\left(5x+1\right)\left(5x+6\right)}=\frac{2005}{2006}\)
\(\Rightarrow1-\frac{1}{6}+\frac{1}{6}-\frac{1}{11}+...+\frac{1}{5x+1}-\frac{1}{5x+6}=\frac{2005}{2006}\)
\(\Rightarrow1-\frac{1}{5x+6}=\frac{2005}{2006}\)
\(\Rightarrow\frac{1}{5x+6}=1-\frac{2005}{2006}\)
\(\Rightarrow\frac{1}{5x+6}=\frac{1}{2006}\)
\(\Rightarrow5x+6=2006\)
\(\Rightarrow5x=2000\)
\(\Rightarrow x=400\)
Vậy x = 400
Trả lời:
\(\frac{x}{2008}-\frac{1}{10}-\frac{1}{15}-\frac{1}{21}-...-\frac{1}{120}=\frac{5}{8}\)
\(\Rightarrow\frac{x}{2008}-\left(\frac{1}{10}+\frac{1}{15}+\frac{1}{21}+...+\frac{1}{120}\right)=\frac{5}{8}\)\(\frac{5}{8}\)
Đặt \(A=\frac{1}{10}+\frac{1}{15}+\frac{1}{21}+...+\frac{1}{120}\), ta được : \(\frac{x}{2008}-A=\frac{5}{8}\) (*)
\(\Rightarrow A=\frac{2}{20}+\frac{2}{30}+\frac{2}{42}+...+\frac{2}{240}\)
\(\Rightarrow A=2\left(\frac{1}{20}+\frac{1}{30}+\frac{1}{42}+...+\frac{1}{240}\right)\)
\(\Rightarrow A=2\left(\frac{1}{4.5}+\frac{1}{5.6}+\frac{1}{6.7}+...+\frac{1}{15.16}\right)\)
\(\Rightarrow A=2\left(\frac{1}{4}-\frac{1}{5}+\frac{1}{5}-\frac{1}{6}+\frac{1}{6}-\frac{1}{7}+...+\frac{1}{15}-\frac{1}{16}\right)\)
\(\Rightarrow A=2\left(\frac{1}{4}-\frac{1}{16}\right)=2.\frac{3}{16}=\frac{3}{8}\)
Thay A vào (*) , ta có:
\(\frac{x}{2008}-\frac{3}{8}=\frac{5}{8}\)
\(\Rightarrow\frac{x}{2008}=1\)
\(\Rightarrow x=2008\)
Vậy x = 2008


mọi người ơi, đây có phải là đáp án đúng của bài 1 không ạ, nếu đúng thì giúp em viết ra giống như trên với ạ, em nhìn được nhưng 1 số chỗ không rõ lắm, huhu

Câu 8:
a:Sửa đề: \(4+4^2+\cdots+4^{2025}\)
Ta có: \(4+4^2+\cdots+4^{2025}\)
\(=\left(4+4^2+4^3\right)+\left(4^4+4^5+4^6\right)+\cdots+\left(4^{2023}+4^{2024}+4^{2025}\right)\)
\(=4\left(1+4+4^2\right)+4^4\left(1+4+4^2\right)+\cdots+4^{2023}\left(1+4+4^2\right)\)
\(=21\left(4+4^4+\cdots+4^{2023}\right)\) ⋮21
b: \(5+5^2+5^3+5^4+\cdots+5^{2024}\)
\(=\left(5+5^2\right)+\left(5^3+5^4\right)+\cdots+\left(5^{2023}+5^{2024}\right)\)
\(=\left(5+5^2\right)+5^2\left(5+5^2\right)+\cdots+5^{2022}\left(5+5^2\right)\)
\(=30\left(1+5^2+\cdots+5^{2022}\right)\) ⋮30
Câu 7:
a: \(A=2+2^2+2^3+\cdots+2^{99}\)
=>\(2A=2^2+2^3+\cdots+2^{100}\)
=>\(2A-A=2^2+2^3+\cdots+2^{100}-2-2^2-\cdots-2^{99}\)
=>\(A=2^{100}-2\)
b: \(B=1-7+7^2-7^3+\cdots+7^{48}-7^{49}\)
=>\(7B=7-7^2+7^3-7^4+\cdots+7^{49}-7^{50}\)
=>\(7B+B=7-7^2+7^3-7^4+\cdots+7^{49}-7^{50}+1-7+7^2-7^3+\cdots+7^{48}-7^{49}\)
=>\(8B=-7^{50}+1\)
=>\(B=\frac{-7^{50}+1}{8}\)
Câu 4:
a: \(x^3=125\)
=>\(x^3=5^3\)
=>x=5
b: \(11^{x+1}=121\)
=>\(11^{x+1}=11^2\)
=>x+1=2
=>x=2-1=1
c: \(\left(x-5\right)^3=27\)
=>\(\left(x-5\right)^3=3^3\)
=>x-5=3
=>x=3+5=8
d: \(4^5:4^{x}=16\)
=>\(4^{x}=4^5:16=4^5:4^2=4^3\)
=>x=3
e: \(5^{x-1}\cdot8=1000\)
=>\(5^{x-1}=1000:8=125=5^3\)
=>x-1=3
=>x=3+1=4
f: \(2^{x}+2^{x+3}=72\)
=>\(2^{x}+2^{x}\cdot8=72\)
=>\(2^{x}\cdot9=72\)
=>\(2^{x}=\frac{72}{9}=8=2^3\)
=>x=3
g: \(\left(3x+1\right)^3=343\)
=>\(\left(3x+1\right)^3=7^3\)
=>3x+1=7
=>3x=6
=>x=2
h: \(3^{x}+3^{x+2}=270\)
=>\(3^{x}+3^{x}\cdot9=270\)
=>\(10\cdot3^{x}=270\)
=>\(3^{x}=\frac{270}{10}=27=3^3\)
=>x=3
i: \(25^{2x+4}=125^{x+3}\)
=>\(\left(5^2\right)^{2x+4}=\left(5^3\right)^{x+3}\)
=>\(5^{4x+8}=5^{3x+9}\)
=>4x+8=3x+9
=>x=1
Câu 6:
1 giờ=3600 giây
Số tế bào hồng cầu được tạo ra sau mỗi giờ là:
\(25\cdot10^5\cdot3600=25\cdot36\cdot10^7=900\cdot10^7=9\cdot10^9\) =9 tỉ (tế bào)
câu 5:
a. \(16^{16}=\left(2^4\right)^{16}=2^{64}\)
\(64^{11}=\left(2^6\right)^{11}=2^{66}\)
vì \(2^{66}>2^{64}\) nên \(64^{11}>16^{16}\)
b. \(625^5=\left(5^4\right)^5=5^{20}\)
\(125^7=\left(5^3\right)^7=5^{21}\)
\(5^{20}<5^{21}\Rightarrow625^5<125^7\)
c. \(3^{36}=\left(3^3\right)^{12}=27^{12}\)
\(5^{24}=\left(5^2\right)^{12}=25^{12}\)
\(27^{12}>25^{12}\Rightarrow3^{36}>5^{24}\)

a) Để \(\frac{7}{n+1}\) đạt giá trị nguyên
<=> 7 \(⋮\) ( n + 1 )
=> n + 1 \(\in\) Ư(7) = { - 7 ; -1 ; 1 ; 7 }
=> n \(\in\) { -8 ; -2 ; 0 ; 6 }
b) Để \(\frac{n+5}{n-2}\) đạt giá trị nguyên
<=> \(n+5⋮n-2\)
=> ( n - 2 ) + 7 \(⋮\) n - 2
=> 7 \(⋮\) n - 2
=> n - 2 \(\in\) Ư(7) = { - 7 ; - 1 ; 1 ; 7 }
=> n \(\in\) { - 5 ; 1 ; 3 ; 9 }
c) Để \(\frac{4n-1}{n-3}\) đạt giá trị nguyên
<=> 4n-1 \(⋮\) n - 3
=> ( 4n - 12 ) + 11 \(⋮\) n- 3
=> 4(n-3) + 11 \(⋮\) n - 3
=> 11 \(⋮\)n - 3
=> n - 3 \(\in\) Ư(11) = { - 11 ; - 1 ; 1 ; 11}
=> n \(\in\) { - 8 ; 2 ; 4 ; 14 }


Câu 8:
a:Sửa đề: \(4+4^2+\cdots+4^{2025}\)
Ta có: \(4+4^2+\cdots+4^{2025}\)
\(=\left(4+4^2+4^3\right)+\left(4^4+4^5+4^6\right)+\cdots+\left(4^{2023}+4^{2024}+4^{2025}\right)\)
\(=4\left(1+4+4^2\right)+4^4\left(1+4+4^2\right)+\cdots+4^{2023}\left(1+4+4^2\right)\)
\(=21\left(4+4^4+\cdots+4^{2023}\right)\) ⋮21
b: \(5+5^2+5^3+5^4+\cdots+5^{2024}\)
\(=\left(5+5^2\right)+\left(5^3+5^4\right)+\cdots+\left(5^{2023}+5^{2024}\right)\)
\(=\left(5+5^2\right)+5^2\left(5+5^2\right)+\cdots+5^{2022}\left(5+5^2\right)\)
\(=30\left(1+5^2+\cdots+5^{2022}\right)\) ⋮30
Câu 7:
a: \(A=2+2^2+2^3+\cdots+2^{99}\)
=>\(2A=2^2+2^3+\cdots+2^{100}\)
=>\(2A-A=2^2+2^3+\cdots+2^{100}-2-2^2-\cdots-2^{99}\)
=>\(A=2^{100}-2\)
b: \(B=1-7+7^2-7^3+\cdots+7^{48}-7^{49}\)
=>\(7B=7-7^2+7^3-7^4+\cdots+7^{49}-7^{50}\)
=>\(7B+B=7-7^2+7^3-7^4+\cdots+7^{49}-7^{50}+1-7+7^2-7^3+\cdots+7^{48}-7^{49}\)
=>\(8B=-7^{50}+1\)
=>\(B=\frac{-7^{50}+1}{8}\)
câu 4:
a) \(\)x³ = 125
x³ = 5³
⇒ x = 5
b. \(11^{x+1}=121\)
\(11^{x+1}=11^2\)
⇒ x + 1 = 2
⇒ x = 2 - 1 = 1
c. (x - 5)³ = 27
(x - 5)³ = 3³
⇒ x - 5 = 3
x = 3 + 5 = 8
d. \(4^5:4^{x}=16\)
\(4^{5-x}=4^2\)
⇒ 5 - x = 2
x = 5 - 2 = 3
e. \(5^{x-1}\cdot8=1000\)
\(5^{x-1}=1000:8\)
\(5^{x-1}=125\)
\(5^{x-1}=5^3\)
⇒ x - 1 = 3
x = 3 + 1 = 4
f. \(2^{x}+2^{x+3}=72\)
\(2^{x}\cdot\left(1+2^3\right)=72\)
\(2^{x}=72:9\)
\(2^{x}=8\)
\(2^{x}=2^3\)
⇒ x = 3
g. (3x + 1)³ = 343
(3x + 1)³ = 7³
⇒ 3x + 1 = 7
3x = 7 - 1
3x = 6
x = 6 : 3 = 2
h. \(3^{x}+3^{x+2}=270\)
\(3^{x}\cdot\left(1+3^2\right)=270\)
\(3^{x}=270:10\)
\(3^{x}=27\)
\(3^{x}=3^3\)
⇒ x = 3
i. \(25^{2x+4}=125^{x+3}\)
\(\left(5^2\right)^{2x+4}=\left(5^3\right)^{x+3}\)
\(5^{4x+8}=5^{3x+9}\)
=>4x + 8 = 3x + 9
4x - 3x = 9 - 8
x = 1


a)
\(175\cdot19+38\cdot175+43\cdot175\\ =175\cdot19+175\cdot38+175\cdot43\\ =175\cdot\left(19+38+43\right)\\ =175\cdot100\\ =17500\)
b)
\(125\cdot75+125\cdot13-80\cdot125\\ =125\cdot75+125\cdot13-125\cdot80\\ =125\cdot\left(75+13-80\right)\\ =125\cdot10\\ =125\cdot8\\ =1000\)
a, 175. 19 + 38. 175 + 43. 175
= 175. 19 + 175. 38 + 175. 43
= 175.(19 + 38 + 43)
= 175. 100
= 17500










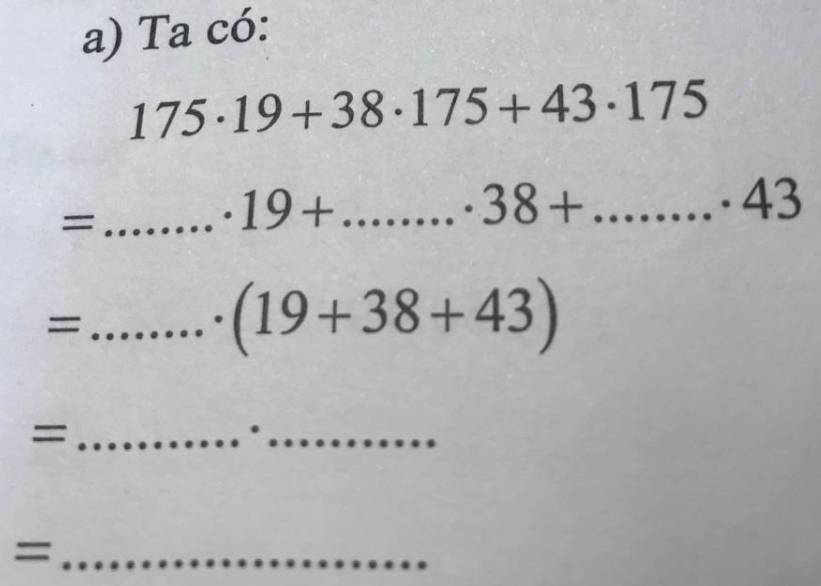
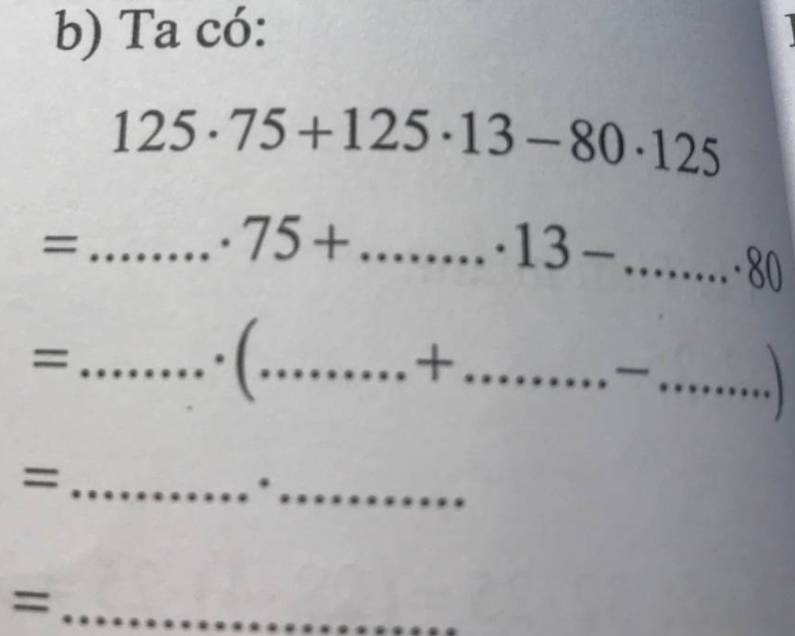
Dạng 3:
Bài 1:
a) Số lượng số hạng là:
\(\left(999-1\right):1+1=999\) (số hạng)
Tổng dãy là:
\(A=\left(999+1\right)\cdot999:2=499500\)
b) Số lượng số hạng là:
\(\left(100-7\right):3+1=32\) (số hạng)
Tổng dãy là:
\(S=\left(100+7\right)\cdot32:2=1712\)