Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

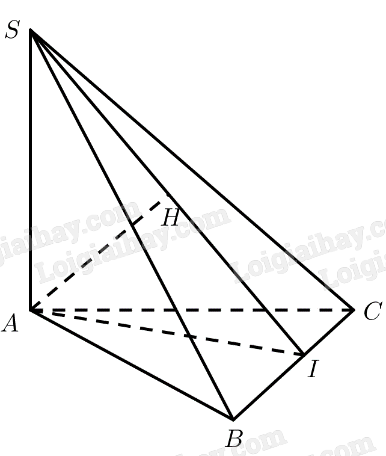
Ta có:
\(\begin{array}{l}\left. \begin{array}{l}SA \bot \left( {ABC} \right) \Rightarrow SA \bot BC\\AI \bot BC\end{array} \right\} \Rightarrow BC \bot \left( {SAI} \right)\\\left. \begin{array}{l} \Rightarrow BC \bot AH\\AH \bot SI\end{array} \right\} \Rightarrow AH \bot \left( {SBC} \right)\end{array}\)
Vậy \(d\left( {A,\left( {SBC} \right)} \right) = AH\).

1:
a: BC vuông góc BA
BC vuông góc SA
=>BC vuông góc (SAB)
b: Kẻ BK vuông góc AC, BH vuông góc SK
=>BH=d(B;(SAC))
\(AC=\sqrt{BA^2+BC^2}=5a\)
AK=(4a)^2/5a=3,2a
BK=4a*3a/5a=2,4a
\(SB=\sqrt{2a^2+16a^2}=3a\sqrt{2}\)
SK=căn 2a^2+10,24a^2=a*3căn 34/5
BK=2,4a
SK^2+BK^2=SB^2
nên ΔSKB vuông tại K
=>K trùng với H
=>d(B;(SAC))=BK=2,4a

1) Ta có : \(SA\perp\left(ABC\right)\Rightarrow SA\perp BC\)
BC \(\perp AB;BC\perp SA\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp SB\) \(\Rightarrow\Delta SBC\perp\) tại B
2) \(BC\perp\left(SAB\right)\Rightarrow BC\perp AH\) . Mà
\(AH\perp SB\Rightarrow AH\perp\left(SBC\right)\Rightarrow AH\perp HK\) \(\Rightarrow\Delta AHK\perp\) tại H
\(\Delta SAB\perp\) tại A ; \(AH\perp SB\) có : \(AH=\dfrac{SA.AB}{\sqrt{SA^2+AB^2}}=\dfrac{a^2}{\sqrt{2a^2}}=\dfrac{\sqrt{2}}{2}a\)
AC = \(\sqrt{AB^2+BC^2}=\sqrt{2a^2}=\sqrt{2}a\)
\(\Delta SAC\perp\) tại A có : \(AK\perp SC\) có :
\(AK=\dfrac{SA.AC}{\sqrt{SA^2+AC^2}}=\dfrac{a.\sqrt{2}a}{\sqrt{a^2+2a^2}}=\dfrac{\sqrt{6}}{3}a\)
\(HK=\sqrt{AK^2-AH^2}=\sqrt{\dfrac{2}{3}a^2-\dfrac{1}{2}a^2}=\dfrac{\sqrt{6}}{6}a\)
\(S_{AHK}=\dfrac{1}{2}HA.HK=\dfrac{1}{2}\dfrac{\sqrt{2}}{2}a.\dfrac{\sqrt{6}}{6}a=\dfrac{\sqrt{3}}{12}a^2\)
3) AH \(\perp\left(SBC\right)\Rightarrow\left(AK;\left(SBC\right)\right)=\widehat{AKH}\)
\(\Delta AHK\perp\) tại H có : \(sin\widehat{AKH}=\dfrac{AH}{AK}=\dfrac{\sqrt{2}}{2}a:\dfrac{\sqrt{6}}{3}a=\dfrac{\sqrt{3}}{2}\Rightarrow\widehat{AKH}=60^o\)

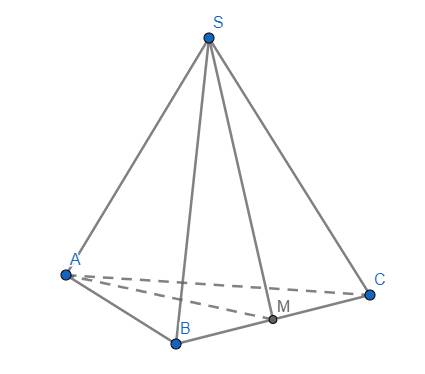
Theo đề bài, dễ có \(\Delta SAB=\Delta SBC=\Delta SCA\left(c.g.c\right)\)
\(\Rightarrow AB=BC=CA\)
Gọi M là trung điểm của BC. Khi đó \(\left\{{}\begin{matrix}SM\perp BC\\AM\perp BC\end{matrix}\right.\) (do các tam giác SBC và ABC lần lượt cân tại S và A). Suy ra \(BC\perp\left(SAM\right)\) \(\Rightarrow BC\perp SA\)
Hoàn toàn tương tự, ta có đpcm.

SA vuông góc (P)
SA vuông góc (ABC)
=>(P)//(ABC)
=>B'C'//BC

a: Sửa đề; BC vuông góc SB
BC vuông góc AB
BC vuông góc SA
=>BC vuôg góc (SAB)
=>CB vuông góc SB
c: (SO;(SCD))=(SO;SK)=góc KSO(OK vuông góc DC tại K)
\(AO=\dfrac{AC}{2}=1.5a\)
\(SA=\sqrt{SC^2-AC^2}=\sqrt{\left(5a\right)^2-\left(3a\right)^2}=4a\)
\(SO=\sqrt{SA^2+AO^2}=\dfrac{a\sqrt{73}}{2}\)
\(AD=BC=\sqrt{\left(3a\right)^2-a^2}=2a\sqrt{2}\)
Xét ΔACD có
O là trung điểm của AC
OK//AD
=>K là trung điểm của CD
=>DK=CK=a/2
\(AK=\sqrt{\left(2a\sqrt{2}\right)^2+\left(\dfrac{a}{2}\right)^2}=\dfrac{a\sqrt{33}}{2}\)
\(SK=\sqrt{SA^2+AK^2}=\sqrt{\left(4a\right)^2+\dfrac{33}{4}a^2}=\dfrac{a\sqrt{97}}{2}\)
OK=AD/2=a căn 2
\(SO=\dfrac{a\sqrt{73}}{2}\)
\(cosKSO=\dfrac{SK^2+SO^2-OK^2}{2\cdot SK\cdot SO}\simeq0.96\)
=>góc KSO=16 độ
Câu c bn ch c/m đc OK vuông góc vs mp (SCD)
Thì sao xác định đc góc cần tìm là OSK

a: BC vuông góc AB
BC vuông góc SA
=>BC vuông góc (SAB)
b: BK vuông góc AC
BK vuôg góc SA
=>BK vuông góc (SAC)


\(SA\perp\left(ABC\right)\Rightarrow SA\perp BC\)
Mà \(BC\perp AI\Rightarrow BC\perp\left(SAI\right)\)
Ta có: \(AH\in\left(SAI\right)\) mà \(BC\perp\left(SAI\right)\Rightarrow BC\perp AH\)
Lại có: \(AH\perp SI\Rightarrow AH\perp\left(SBC\right)\)
\(\Rightarrow AH\perp SC\)
Cảm ơn bạn ạ