
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ĐK: 2x -1 ≥ 0 ⇔ x ≥ \(\frac{1}{2}\)
\(\left(x-1\right)\sqrt{2x-1}=3\left(x^2-5x+4\right)\)
⇔ (x -1)\(\sqrt{2x-1}\) = 3(x - 4)(x - 1)
- Xét x = 1 ta thấy là nghiệm của phương trình (1)
- Xét x≠ 1: \(\sqrt{2x-1}=3\left(x-4\right)\) (x ≥ 4)
⇔ 2x -1 = 9x2 -72x + 144
⇔\(\left[{}\begin{matrix}x=5\left(TM\right)\left(2\right)\\x=\frac{29}{9}\left(KTM\right)\end{matrix}\right.\)
Từ (1), (2) suy ra nghiệm của phương trình là \(\left[{}\begin{matrix}x=1\\x=5\end{matrix}\right.\)

Uh mình chỉ giúp được câu a
\(x^2-5x+3=0\)
\(\Delta=b^2-4ac\)
\(=\left(-5\right)^2-4.1.3\)
\(=25-12=13>0\)
\(x1=\dfrac{b+\sqrt{\Delta}}{2a}=\dfrac{5+\sqrt{13}}{2}\)
\(x2=\dfrac{b-\sqrt{\Delta}}{2a}=\dfrac{5-\sqrt{13}}{2}\)

\(2^a3^b=\frac{4}{3}\Leftrightarrow2^a.3^{b+1}=4\Leftrightarrow\frac{2^a3^{b+1}}{2^2}=1\Leftrightarrow2^{a-2}3^{b+1}=1.\)
vì 2 và ba nguyên tố cùng nhau nên : \(2^{a-2}.3^{b+1}=1\Leftrightarrow\hept{\begin{cases}a-2=0\\b+1=0\end{cases}\Leftrightarrow\hept{\begin{cases}a=2\\b=-1\end{cases}.}}\)
HOẶC
\(\left(2^{a-2}.3^{b+1}=1\Leftrightarrow2^{a-2}.3^{b+1}=2^0.3^0\Rightarrow\hept{\begin{cases}a-2=0\\b+1=0\end{cases}\Rightarrow}\hept{\begin{cases}a=2\\b=-1\end{cases}}.\right)\)

Ta có: \(xyz\le\left(\frac{x+y+z}{3}\right)^3=\frac{1}{27}\) và \(\left(x+y\right)\left(y+z\right)\left(z+x\right)\le\left(\frac{x+y+y+z+z+x}{3}\right)^3=\frac{8}{27}\)
\(\Rightarrow B\le\frac{1}{27}.\frac{8}{27}=\frac{8}{729}\Rightarrow k=\frac{8}{729}\Rightarrow9^3.k=8\)

MỤC ĐÍCH CỦA MÀY LÀ QUẢNG CÁO NHẠC THÌ YÊU CẦU CÚT OK?
CÒN NẾU MÀY MÀY MUỐN HỎI THẬT SỰ THÌ XIN MÀY CHỈ GÕ ĐỀ TOÁN VÀ ĐỪNG CHO THÊM MẤY THỨ TẠP CHẤT KIA VÀO.
CHỨ KHÔNG PHẢI LÀ HỎI MỘT CÁCH CHỐNG CHẾ KIA NHÉ


\(\sqrt{\frac{x^2+4y^2}{2}}+\sqrt{\frac{x^2+2xy+4y^2}{3}}=\sqrt{\frac{x^2}{2}+\frac{4y^2}{2}}+\sqrt{\frac{\left(x+y\right)^2}{3}+\frac{y^2}{1}}\)
\(\ge\sqrt{\frac{\left(x+2y\right)^2}{2+2}}+\sqrt{\frac{\left(x+y+y\right)^2}{3+1}}=\frac{x+2y}{2}+\frac{x+2y}{2}=x+2y\)

Áp dụng BĐT cauchy, ta có:
\(\sqrt{\left(2y+2z-x\right)\cdot3x}\le\dfrac{2z+2y-x+3x}{2}=\dfrac{2\left(x+y+z\right)}{2}=x+y+z\\ \Leftrightarrow\sqrt{2y+2z-x}\le\dfrac{x+y+z}{\sqrt{3x}}\\ \Leftrightarrow\sqrt{\dfrac{x}{2y+2z-x}}\ge\dfrac{\sqrt{x}}{\dfrac{x+y+z}{\sqrt{3x}}}=\dfrac{x\sqrt{3}}{x+y+z}\)
\(\Leftrightarrow S=\sum\sqrt{\dfrac{x}{2y+2z-x}}\ge\sqrt{3}\left(\dfrac{x}{x+y+z}+\dfrac{y}{x+y+z}+\dfrac{z}{x+y+z}\right)\\ \Leftrightarrow S\ge\sqrt{3}\cdot\dfrac{x+y+z}{x+y+z}=\sqrt{3}\)
Dấu \("="\Leftrightarrow x=y=z\) hay tam giác đều

4:
a: góc CEH+góc CDH=180 độ
=>CDHE nội tiếp
b: Xét ΔHEA vuông tại E và ΔHDB vuông tại D có
góc EHA=góc DHB
=>ΔHEA đồng dạng với ΔHDB
=>HE/HD=HA/HB
=>HE*HB=HD*HA

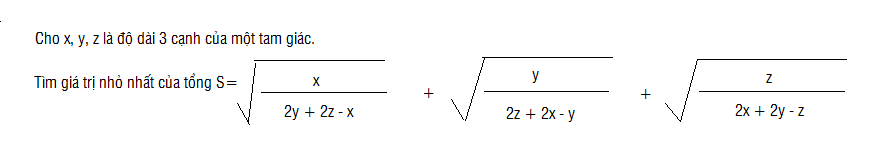
 mọi người giải hộ em với ạ,em cảm ơn
mọi người giải hộ em với ạ,em cảm ơn
\(C=\left(\frac{1}{x+\sqrt{x}}-\frac{1}{\sqrt{x}+1}\right):\frac{\sqrt{x}-1}{x+2\sqrt{x}+1}\)
\(=\frac{1-x}{\left(x+\sqrt{x}\right)\left(\sqrt{x}+1\right)}.\frac{\left(\sqrt{x}+1\right)^2}{\sqrt{x}-1}\)
\(=-\frac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)}=-\frac{\sqrt{x}+1}{\sqrt{x}}\)