
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xét tứ giác ABCD có:
\(\begin{array}{l} \widehat A + \widehat B + \widehat C + \widehat D = {360^0}\\{85^0} + x + {65^0} + {75^0} = {360^0}\\x = {360^0} - {85^0} - {65^0} - {75^0} = {135^0}\end{array}\)

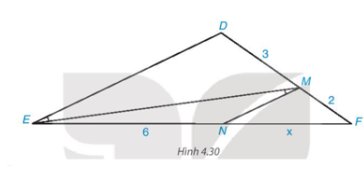
Trong Hình 4.30 có \(\widehat {DEM} = \widehat {EMN}\) mà hai góc này ở vị trí so le trong nên MN // DE.
Áp dụng định lí Thalès vào tam giác DEF có MN // DE, ta có:
\(\dfrac{{MF}}{{M{\rm{D}}}} = \dfrac{{NF}}{{NE}}\) hay \(\dfrac{2}{3} = \dfrac{x}{6}\)
Suy ra \(x = \dfrac{{2.6}}{3} = 4\) (đvđd).
Vậy x = 4 (đvđd).


a: Xét tứ giác DIHK có
góc DIH=góc DKH=góc KDI=90 độ
nên DIHK là hình chữ nhật
b: Xét tứ giác IHAK có
IH//AK
IH=AK
Do đó: IHAK là hình bình hành
=>B là trung điểm chung của IA và HK
Xét ΔIKA có IC/IK=IB/IA
nên BC//KA
Xét ΔIDA có IB/IA=IM/ID
nên BM//DA
=>B,C,M thẳng hàng

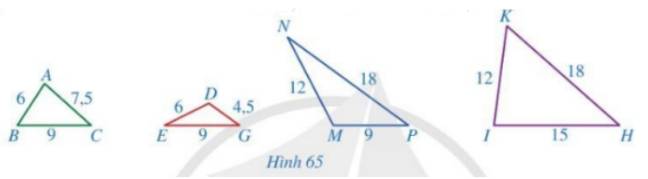
Xét tam giác ABC và tam giác IKH có:
\(\frac{{AB}}{{IK}} = \frac{{AC}}{{IH}} = \frac{{BC}}{{KH}} = \frac{1}{2}\)
\( \Rightarrow \Delta ABC \backsim\Delta IKH\) (c-c-c)
Xét tam giác DEG và tam giác MNP có:
\(\frac{{DE}}{{MN}} = \frac{{DG}}{{MP}} = \frac{{EG}}{{KH}} = \frac{1}{2}\)
\( \Rightarrow \Delta DEG \backsim\Delta MNP\) (c-c-c)

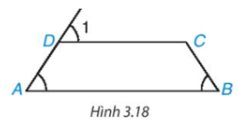
Ta có \(\widehat A = \widehat {{D_1}}\) mà hai góc này ở vị trí đồng vị nên AB // CD.
Suy ra tứ giác ABCD là hình thang.
Mặt khác hình thang ABCD có \(\widehat A = \widehat B\) nên ABCD là hình thang cân.
Do đó AD = BC (đpcm).

\({x^6} + {y^6} = {\left( {{x^2}} \right)^3} + {\left( {{y^2}} \right)^3} = \left( {{x^2} + {y^2}} \right)\left[ {{{\left( {{x^2}} \right)}^2} - {x^2}.{y^2} + {{\left( {{y^2}} \right)}^2}} \right] = \left( {{x^2} + {y^2}} \right)\left( {{x^4} - {x^2}{y^2} + {y^4}} \right)\)

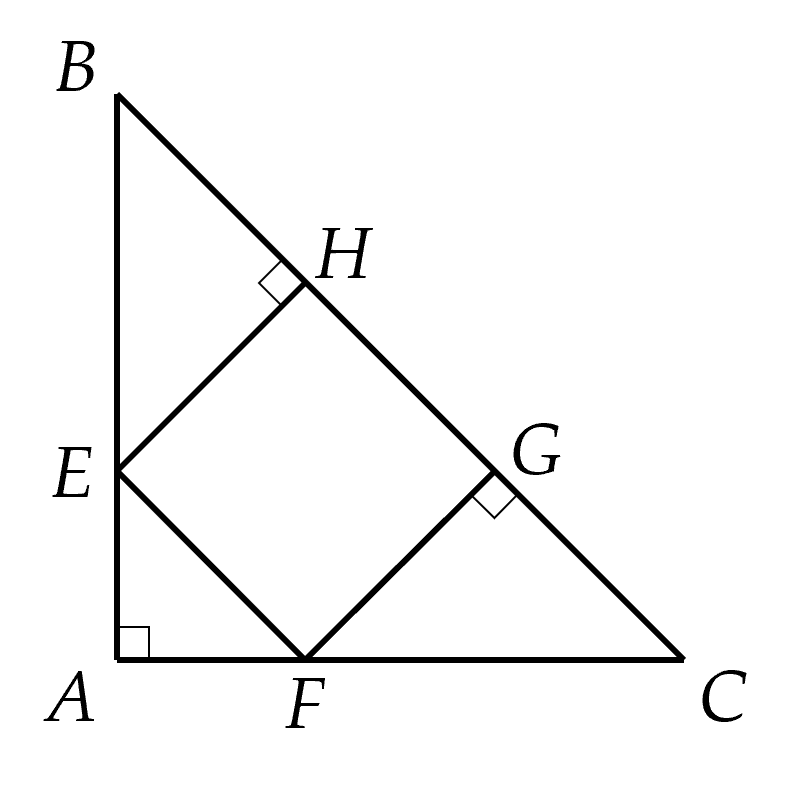
a) Δ��� Tam giác ABC vuông cân nên góc B= góc C = 45 độ
Tam giácBHE vuông tại H có góc BEH + góc B = 90 độ
Suy ra góc BEH = 90 độ - 45 độ = 45 độ nên góc B= góc BEH = 45 độ
Vậy tam giác BEH vuông tại H
b) Chứng minh tương tự như câu a ta được tam giác CFG vuông tại G nên GF=GC và HB=HE
Lại có BH=HG=GC suy ra EH=HG=GF và EH//FG ( cùng vuông góc với BC)
Tứ giác EFGH có EH//FG, EH=FG
=>tứ giác EFGH là hình bình hành
Xét hình bình hành có một góc vuông là góc H nên là hình chữ nhật
Mà hình chữ nhật có hai cạnh kề bằng nhau là EH=HG nên là hình vuông
Vậy EFGH là hình vuông
a) Δ���ΔABC vuông cân nên �^=�^=45∘.B=C=45∘.
Δ���ΔBHE vuông tại �H có ���^+�^=90∘BEH+B=90∘
Suy ra ���^=90∘−45∘=45∘BEH=90∘−45∘=45∘ nên �^=���^=45∘B=BEH=45∘.
Vậy Δ���ΔBEH vuông cân tại �.H.
b) Chứng minh tương tự câu a ta được Δ���ΔCFG vuông cân tại �G nên ��=��GF=GC và ��=��HB=HE
Mặt khác ��=��=��BH=HG=GC suy ra ��=��=��EH=HG=GF và ��EH // ��FG (cùng vuông góc với ��)BC)
Tứ giác ����EFGH có ��EH // ��,��=��FG,EH=FG nên là hình bình hành.
Hình bình hành ����EFGH có một góc vuông �^H nên là hình chữ nhật
Hình chữ nhật ����EFGH có hai cạnh kề bằng nhau ��=��EH=HG nên là hình vuông.

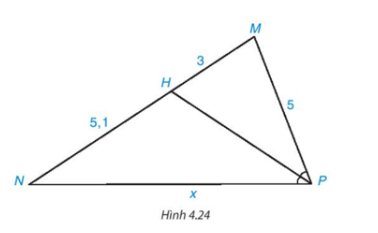
Trong Hình 4.24 có \(\widehat {MPH} = \widehat {NPH}\) nên PH là tia phân giác của \(\widehat {MPN}\).
Áp dụng tính chất đường phân giác của tam giác, ta có:
\(\dfrac{{MP}}{{NP}} = \dfrac{{MH}}{{NH}}\) hay \(\dfrac{5}{x} = \dfrac{3}{{5,1}}\)
Suy ra \(x = \dfrac{{5.5,1}}{3} = 8,5\) (đvđd).
Vậy x = 8,5 (đvđd).







2.26:
a. $x^2-6x+9-y^2=(x^2-6x+9)-y^2=(x-3)^2-y^2$
$=(x-3-y)(x-3+y)$
b. $4x^2-y^2+4y-4=4x^2-(y^2-4y+4)$
$=(2x)^2-(y-2)^2=(2x-y+2)(2x+y-2)$
c. $xy+z^2+xz+yz=(xy+xz)+(z^2+yz)=x(y+z)+z(z+y)$
$=(y+z)(x+z)$
c.
$x^2-4xy+4y^2+xz-2yz$
$=(x^2-4xy+4y^2)+(xz-2yz)$
$=(x-2y)^2+z(x-2y)=(x-2y)(x-2y+z)$
2.27:
a. $x^3+y^3+x+y=(x^3+y^3)+(x+y)$
$=(x+y)(x^2-xy+y^2)+(x+y)=(x+y(x^2-xy+y^2+1)$
b. $x^3-y^3+x-y=(x^3-y^3)+(x-y)=(x-y)(x^2+xy+y^2)+(x-y)$
$=(x-y)(x^2+xy+y^2+1)$
c.
$(x-y)^3+(x+y)^3=(x^3-3x^2y+3xy^2-y^3)+(x^3+3x^2y+3xy^2+y^3)$
$=2x^3+6xy^2=2x(x^2+3y^2)$
d.
$x^3-3x^2y+3xy^2-y^3+y^2-x^2$
$=(x^3-3x^2y+3xy^2-y^3)-(x^2-y^2)$
$=(x-y)^3-(x-y)(x+y)=(x-y)[(x-y)^2-(x+y)]$
$=(x-y)(x^2-2xy+y^2-x-y)$