Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Hình thang ABCD (AB song song CD) có AB=10, BD=6, MN= 4 (M,N là trung điểm AB,CD). Tính \(S_{ABCD}\)


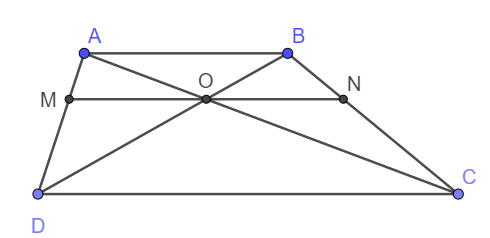
a) Do AB//CD nên áp dụng hệ quả định lý Ta let ta có:
\(\frac{AO}{OC}=\frac{OB}{OD}\) hay \(\frac{DO}{DB}=\frac{OC}{AC}\)
Xét tam giác ABD có OM//AB nên \(\frac{OM}{AB}=\frac{DO}{DB}\)
Tương tự \(\frac{ON}{AB}=\frac{CO}{CA}\)
Vậy nên \(\frac{OM}{AB}=\frac{ON}{AB}\Rightarrow OM=ON\)
b) Coi AB = 1, DC = k thì \(\frac{DO}{OB}=\frac{DC}{AB}=k\Rightarrow\frac{DO}{DB}=\frac{k}{k+1}\)
\(\Rightarrow OM=ON=\frac{k}{k+1}\Rightarrow MN=\frac{2k}{k+1}\)
Ta có \(\frac{1}{AB}+\frac{1}{CD}=\frac{1}{1}+\frac{1}{k}=\frac{k+1}{k}\)
\(\frac{2}{MN}=\frac{2}{\frac{2k}{k+1}}=\frac{k+1}{k}\)
Vậy nên \(\frac{1}{AB}+\frac{1}{CD}=\frac{2}{MN}\)
c) Ta thấy ngay \(\Delta COD\sim\Delta AOB\left(g-g\right)\) theo tỉ lệ k ở câu b.
Vậy thì \(\frac{S_{COD}}{S_{AOB}}=\frac{2009^2}{2008^2}=\left(\frac{2009}{2008}\right)^2=k^2\Rightarrow k=\frac{2009}{2008}\)
Từ đó ta có \(\frac{OC}{OA}=\frac{DO}{OB}=\frac{2009}{2008}\)
Vậy thì \(\frac{S_{ADO}}{S_{AOB}}=\frac{2009}{2008}\Rightarrow S_{ADO}=\frac{2009}{2008}.2008^2=2009.2008\)
\(\frac{S_{BOC}}{S_{AOB}}=\frac{2009}{2008}\Rightarrow S_{BOC}=\frac{2009}{2008}.2008^2=2009.2008\)
Suy ra \(S_{ABCD}=S_{AOB}+S_{DOC}+S_{AOD}+S_{BOC}=2008^2+2009^2+2.2008.2009\)
\(=\left(2008+2009\right)^2=4017^2\left(cm^2\right)\)

Không mất tính tổng quát, giả sử AB < CD
Gọi K là giao điểm của AD và BC
Dễ có: \(\Delta KEF~\Delta KAB\left(g.g\right)\Rightarrow\frac{S_{KAB}}{S_{KEF}}=\frac{AB^2}{EF^2}\)(tỉ số diện tích bằng bình phương tỉ số đồng dạng)
\(\Delta KEF~\Delta KDC\left(g.g\right)\Rightarrow\frac{S_{KDC}}{S_{KEF}}=\frac{CD^2}{EF^2}\)(tỉ số diện tích bằng bình phương tỉ số đồng dạng)
Từ đó suy ra \(\frac{AB^2+CD^2}{EF^2}=\frac{S_{KAB}+S_{KCD}}{S_{KEF}}=\frac{\left(S_{KAB}+S_{ABFE}\right)+\left(S_{KCD}-S_{EFCD}\right)}{S_{KEF}}=2\)\(\Rightarrow EF^2=\frac{AB^2+CD^2}{2}\)hay \(EF=\sqrt{\frac{AB^2+CD^2}{2}}\)(đpcm)