
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


hình bạn tự vẽ nha
giả sử : góc AOC \(\le\) góc BOC
Các điểm O, E,M,F thuộc đường tròn đường kính OM=R
Các điểm O,G,N,H thuộc đường tròn đường kính ON=R
Trong 2 đường tròn bằng nhau đó, góc nội tiếp EOF = góc nội tiếp GNH(cùng bù với góc NOH)
nên góc EF = góc GH
=>EF=GH




Câu 10:
Gọi \(H\) là giao điểm của \(MO\) và \(AB\).
Xét tam giác \(MAO\) vuông tại \(A\) đường cao \(AH\):
\(\dfrac{1}{AH^2}=\dfrac{1}{MA^2}+\dfrac{1}{AO^2}\Leftrightarrow\dfrac{1}{\left(\dfrac{R\sqrt{2}}{2}\right)^2}=\dfrac{1}{MA^2}+\dfrac{1}{R^2}\Leftrightarrow MA=R\).
\(S_{MAOB}=S_{MAO}+S_{MBO}\)
\(=\dfrac{1}{2}.AO.MA+\dfrac{1}{2}.OB.MB\)
\(=\dfrac{1}{2}.R.R+\dfrac{1}{2}.R.R=R^2\)
Chọn C.

Đài ơi, giải giúp cho Sarah đi, tớ không có viết và giờ vào giường rồi , good nigh

Lời giải:
Gọi vận tốc ban đầu là $x$ km/h
Thời gian dự định: $\frac{AB}{x}$ (h)
Khi vận tốc tăng $a$ km/h thì thời gian đi là: $\frac{AB}{x+a}$ (h)
$\frac{AB}{x}-\frac{AB}{x+a}=0,5$
$\Leftrightarrow \frac{aAB}{x(x+a)}=0,5(*)$
Khi vận tốc giảm $b$ km/h thì thời gian đi là: $\frac{AB}{x-b}$ (h)
$\frac{AB}{x-b}-\frac{AB}{x}=1$
$\Leftrightarrow \frac{bAB}{x(x-b)}=1(**)$
Từ $(*); (**)\Rightarrow \frac{x-b}{x+a}.\frac{a}{b}=0,5$
$\Leftrightarrow 2a(x-b)=b(x+a)$
$\Leftrightarrow 2ax-2ab=bx+ab$
$\Leftrightarrow x(2a-b)=3ab$
$\Rightarrow x=\frac{3ab}{2a-b}$
Đến đây bạn thay $a,b$ vô để tính thôi.

1)
a) \(2\sqrt{50}-3\sqrt{2}+\dfrac{1}{3}\sqrt{18}\)
\(=2\cdot5\sqrt{2}-3\sqrt{2}+\dfrac{1}{3}\cdot3\sqrt{2}\)
\(=10\sqrt{2}-3\sqrt{2}+\sqrt{2}\)
\(=8\sqrt{2}\)
b) \(\dfrac{11}{4-\sqrt{5}}-\dfrac{3}{\sqrt{5}+\sqrt{2}}\)
\(=\dfrac{11\left(4+\sqrt{5}\right)}{\left(4-\sqrt{5}\right)\left(4+\sqrt{5}\right)}-\dfrac{3\left(\sqrt{5}-\sqrt{2}\right)}{\left(\sqrt{5}+\sqrt{2}\right)\left(\sqrt{5}-\sqrt{2}\right)}\)
\(=\dfrac{11\left(4+\sqrt{5}\right)}{16-5}-\dfrac{3\left(\sqrt{5}-\sqrt{2}\right)}{5-2}\)
\(=\dfrac{11\left(4+\sqrt{5}\right)}{11}-\dfrac{3\left(\sqrt{5}-\sqrt{2}\right)}{3}\)
\(=4+\sqrt{5}-\sqrt{5}+\sqrt{2}\)
\(=4+\sqrt{2}\)
c) \(\sqrt{8-2\sqrt{15}}-\sqrt{\left(\sqrt{5}+\sqrt{3}\right)^2}\)
\(=\sqrt{\left(\sqrt{5}\right)^2-2\cdot\sqrt{5}\cdot\sqrt{3}+\left(\sqrt{3}\right)^2}-\sqrt{\left(\sqrt{5}+\sqrt{3}\right)^2}\)
\(=\sqrt{\left(\sqrt{5}-\sqrt{3}\right)^2}-\sqrt{\left(\sqrt{5}+\sqrt{3}\right)^2}\)
\(=\left|\sqrt{5}-\sqrt{3}\right|-\left|\sqrt{5}+\sqrt{3}\right|\)
\(=\sqrt{5}-\sqrt{3}-\sqrt{5}-\sqrt{3}\)
\(=-2\sqrt{3}\)




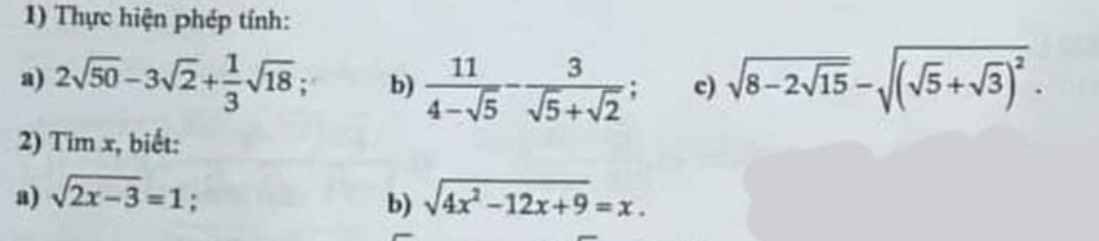
gọi số hàng chục là X hàng đơn vị là Y
theo đề bái có: X+Y=7 (1)
nếu đổi chỗ thì được 1 số hơn số ban đầu là 27 nên ta có:
(10Y+X)-(10X+Y)=27 (2)
có hệ phương trình
X+Y=7
(10Y+X)-(10X+Y)=27
==>giải hệ phương trình được X=2 và Y= 5
cảm ơn b nhaa