K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
3 tháng 7 2020
Phương trình tham số d1: \(\left\{{}\begin{matrix}x=1+2t\\y=3+3t\\z=2t\end{matrix}\right.\)
Phương trình tham số d2: \(\left\{{}\begin{matrix}x=5+6t'\\y=4t'\\z=5-5t'\end{matrix}\right.\)
Gọi (Q) là mặt phẳng song song (P) và cách (P) 1 khoảng bằng 2 \(\Rightarrow\) pt có dạng \(x-2y-2z-d=0\) (\(d\ne1\))
Gọi \(A\left(d;0;0\right)\) là 1 điểm thuộc (Q)
\(d\left(A;\left(P\right)\right)=2\Leftrightarrow\frac{\left|d+1\right|}{\sqrt{1+4+4}}=2\Leftrightarrow\left|d+1\right|=6\Rightarrow\left[{}\begin{matrix}d=5\\d=-7\end{matrix}\right.\)
Có 2 mp (Q) thỏa mãn: \(\left[{}\begin{matrix}x-2y-2z-5=0\\x-2y-2z+7=0\end{matrix}\right.\)
M là giao điểm (Q) và d1 nên tọa độ M là ...
N là giao điểm (Q) và d2 nên tọa độ N là ...
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 12 2020
\(\overrightarrow{NM}=\left(4;-2;2\right)=2\left(2;-1;1\right)\)
Gọi Q là trung điểm MN \(\Rightarrow Q\left(-1;3;2\right)\)
Phương trình mặt phẳng trung trực của MN (đi qua Q và nhận \(\overrightarrow{NM}\) là 1 vecto pháp tuyến) có dạng:
\(2\left(x+1\right)-1\left(y-3\right)+1\left(z-2\right)=0\)
\(\Leftrightarrow2x-y+z+3=0\)
b.
(P) có 1 vecto pháp tuyến là \(\left(1;2;-1\right)\)
Do \(\left(\beta\right)\) song song (P) nên cũng nhận \(\left(1;2;-1\right)\) là 1 vtpt
À thôi bạn ghi sai đề rồi, \(\left(\beta\right)\) chỉ có thể đi qua M hoặc N (1 điểm thôi), không thể đi qua MN được vì MN không song song với (P)
29 tháng 4 2020
Bài 1:
a) Ta có: \(\left(x+5\right)^2=100\)
\(\Leftrightarrow\left[{}\begin{matrix}x+5=10\\x+5=-10\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\\x=-15\end{matrix}\right.\)
Vậy: \(x\in\left\{5;-15\right\}\)
b) Ta có: \(\left(2x-4\right)^2=0\)
\(\Leftrightarrow2x-4=0\)
\(\Leftrightarrow2x=4\)
hay x=2
Vậy: x=2
c) Ta có: \(\left(x-1\right)^3=27\)
\(\Leftrightarrow x-1=3\)
hay x=4
Vậy: x=4
29 tháng 4 2020
Cảm ơn anh nhiều ạ,chiều nay hok trực tuyến mà ko lm đc,may mà có anh gp em
AH
Akai Haruma
Giáo viên
1 tháng 3 2017
Bài 1)
Gọi số phức $z$ có dạng \(z=a+bi(a,b\in\mathbb{R})\).
Ta có \(|z|+z=3+4i\Leftrightarrow \sqrt{a^2+b^2}+a+bi=3+4i\)
\(\Rightarrow\left\{\begin{matrix}\sqrt{a^2+b^2}+a=3\\b=4\end{matrix}\right.\Rightarrow\left\{\begin{matrix}a=\frac{5}{6}\\b=4\end{matrix}\right.\)
Vậy số phức cần tìm là \(\frac{5}{6}+4i\)
b)
\(\left\{\begin{matrix} z_1+3z_1z_2=(-1+i)z_2\\ 2z_1-z_2=3+2i\end{matrix}\right.\Rightarrow \left\{\begin{matrix} \frac{z_1}{z_2}+3z_1=-1+i\\ 2z_1-z_2=3+2i\end{matrix}\right.\Rightarrow \frac{z_1}{z_2}+z_1+z_2=(-1+i)-(3+2i)=-4-i\)
\(\Leftrightarrow w=-4-i\Rightarrow |w|=\sqrt{17}\)
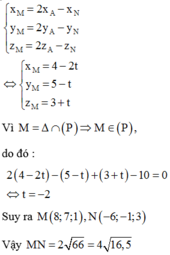
Đáp án:
=2
HT