
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 6:
a: =12x^2+4x-3x-1-5x^2+15x-x^2+7x-12
=6x^2+23x-13
b: =5x^2+5x-2x-2-3x^3+3x^2+9x-2x(x^2-9x+20)
=-3x^3+8x^2+14x-2-2x^3+18x^2-40x
=-5x^3+26x^2-26x-2

| x-2/3| = 1/3+2/5
= 11/15
=> x-2/3=11/15 hoặc x-2/3=-11/15
x= 7/5 x = -1/15
k cho mk nha
\(\left|x-\frac{2}{3}\right|-\frac{2}{5}=\frac{1}{3}\)
\(\Rightarrow\left|x-\frac{2}{3}\right|=\frac{1}{3}+\frac{2}{5}=\frac{11}{15}\)
\(\Rightarrow\orbr{\begin{cases}\Rightarrow x-\frac{2}{3}=\frac{11}{15}\\x-\frac{2}{3}=\frac{-11}{15}\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}\Rightarrow x=\frac{7}{15}\\x=\frac{-1}{15}\end{cases}}\)

Câu 5:
Ta thấy \(\left(x-2\right)^2\ge0\Rightarrow A\ge-1\)
Dấu "=" xảy ra khi \(\left(x-2\right)^2=0\Leftrightarrow x-2=0\Leftrightarrow x=2\)

Bài 11:
a) Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
Do đó: ΔBAD=ΔBED(Cạnh huyền-góc nhọn)
Suy ra: BA=BE(Hai cạnh tương ứng) và DA=DE(Hai cạnh tương ứng)
Ta có: BA=BE(cmt)
nên B nằm trên đường trung trực của AE(1)
Ta có: DA=DE(cmt)
nên D nằm trên đường trung trực của AE(2)
Từ (1) và (2) suy ra BD là đường trung trực của AE(đpcm)

Ta có:
( -64 )7 = ((-4)4)7 = (-4)28 = 428
( -16)11 = (42)11 = 422
Vì 428 > 422 nên (-64)7 > (-16)11
( chỗ có 2 dấu ngoặc tròn"(" thì thay bằng dấu ngoặc vuông nha )
ta so sánh :
647 và 1611
647 = ( 43 )7 = 421
1611 = ( 42 )11 = 422
\(\Rightarrow\)647 < 1611
\(\Rightarrow\)( -64 )7 > ( -16 )11

a. f(\(\dfrac{-1}{2}\)) = \(4.\left(\dfrac{-1}{2}\right)^2+3.\left(\dfrac{-1}{2}\right)-2\)
= \(4.\dfrac{1}{4}-\left(\dfrac{-3}{2}\right)-\dfrac{4}{2}\)
= \(\dfrac{2}{2}+\dfrac{3}{2}-\dfrac{4}{2}\)
= \(\dfrac{1}{2}\)

Bạn cần hỗ trợ bài nào thì nên chụp nguyên bài đó ra thôi. Nếu bạn cần giúp nhiều bài thì nên tách lẻ mỗi bài mỗi post hoặc 2 bài/ post. Bạn chụp như thế này gây "ngợp" nên sẽ ít ai dừng lại và hỗ trợ.

5: \(=\dfrac{1}{2}\cdot10-\dfrac{1}{2}=\dfrac{1}{2}\cdot9=\dfrac{9}{2}\)
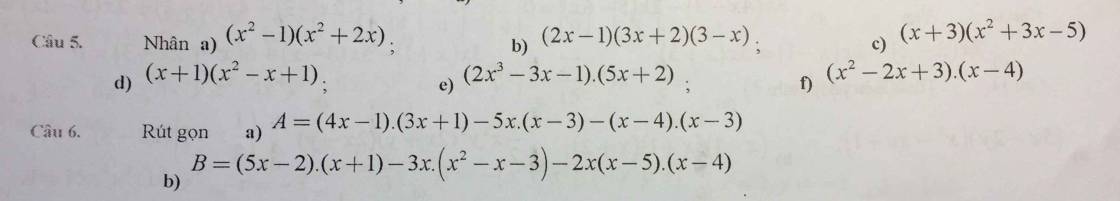
 giúp mk với mn mk đang gấp
giúp mk với mn mk đang gấp
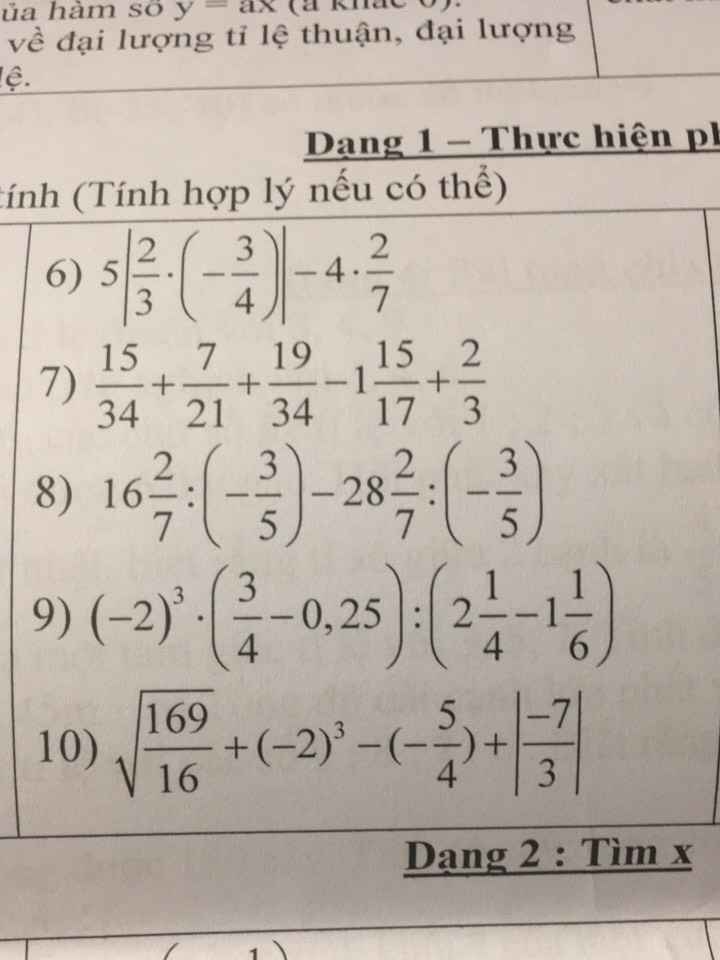
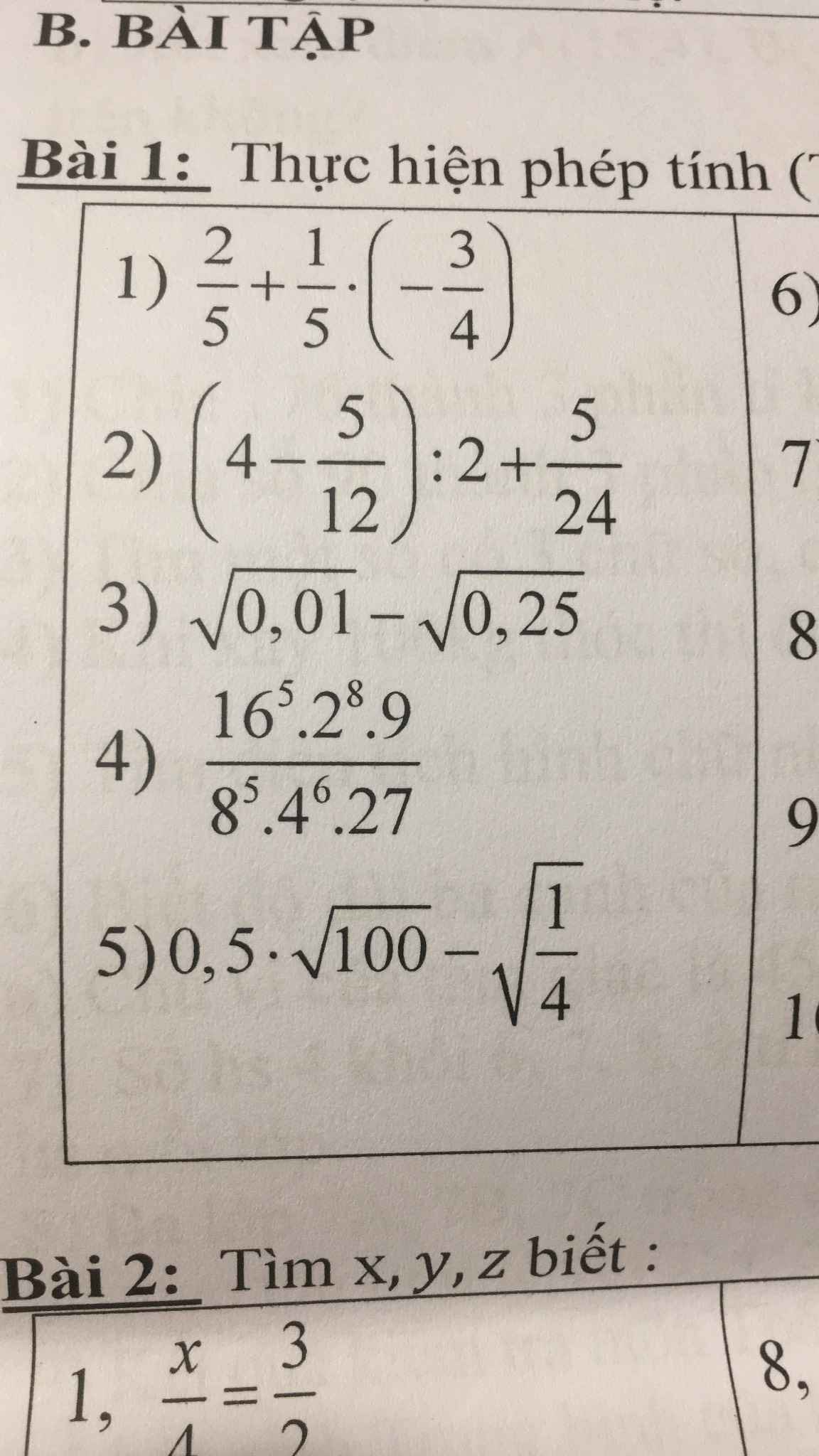
\(a.\) Xét \(\Delta AEM\) vuông tại E và \(\Delta AFM\) vuông tại F:
\(\widehat{EAM}=\widehat{FAM}\) \((\)AM là phân giác \(\widehat{BAC}\)\().\)
\(AM\) \(chung.\)
\(\Rightarrow\) \(\Delta AEM\) \(=\Delta AFM\left(ch-gn\right).\)
\(b.\) Xét \(\Delta BEM\) vuông tại E:
BE; EM là 2 cạnh góc vuông.
BM là cạnh huyền.
\(\Rightarrow\) \(BM>BE;ME.\)
Vì \(\Delta AEM\) \(=\Delta AFM\left(cmt\right).\)
\(\Rightarrow ME=MF\) (2 cạnh tương ứng).
Mà \(BM>ME.\)
\(\Rightarrow BM>MF.\)