Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}3x^2-2x-1=0\\y=3x^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x^2-3x+x-1=0\\y=3x^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x-1\right)\left(3x+1\right)=0\\y=3x^2\end{matrix}\right.\Leftrightarrow\left(x,y\right)\in\left\{\left(1;3\right);\left(-\dfrac{1}{3};\dfrac{1}{3}\right)\right\}\)

a: Thay x=-2 vào y=-3x+4, ta được:
y=6+4=10
Thay x=-2 và y=10 vào hàm số \(y=ax^2\), ta được:
\(4a=10\)
hay a=5/2
c: (P): y=5/2x2
(d): y=-3x+4
Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}\dfrac{5}{2}x^2+3x-4=0\\y=-3x+4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5x^2+6x-8=0\\y=-3x+4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}5x^2+10x-4x-8=0\\y=-3x+4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(x+2\right)\left(5x-4\right)=0\\y=-3x+4\end{matrix}\right.\)
\(\Leftrightarrow\left(x,y\right)\in\left\{\left(-2;10\right);\left(\dfrac{4}{5};\dfrac{8}{5}\right)\right\}\)

\(a,\Leftrightarrow a+3=4\Leftrightarrow a=1\\ \Leftrightarrow y=x+3\\ c,\text{PT hoành độ giao điểm: }x+3=2x+5\Leftrightarrow x=-2\Leftrightarrow y=1\Leftrightarrow A\left(-2;1\right)\\ \text{Vậy tọa độ giao điểm 2 đths là }A\left(-2;1\right)\)

Đầu tiên là vì điểm M \(\in\) y=ax2
=> Thay x và y của toạ độ điểm M vào pt y=ax2
=> Tìm ra a
=>Thay lại pt ban đầu
=> Kẻ bảng và vẽ parabol như bình thường

a: Thay x=-2 và y=1 vào (P), ta được:
4a=1
hay a=1/4
b: KHi y=9 thì 1/4x2=9
=>x=6 hoặc x=-6

a) Hàm số y=ax2 đi qua điểm (-1;3) nên
=> 3==a(-1)2
=> a=3
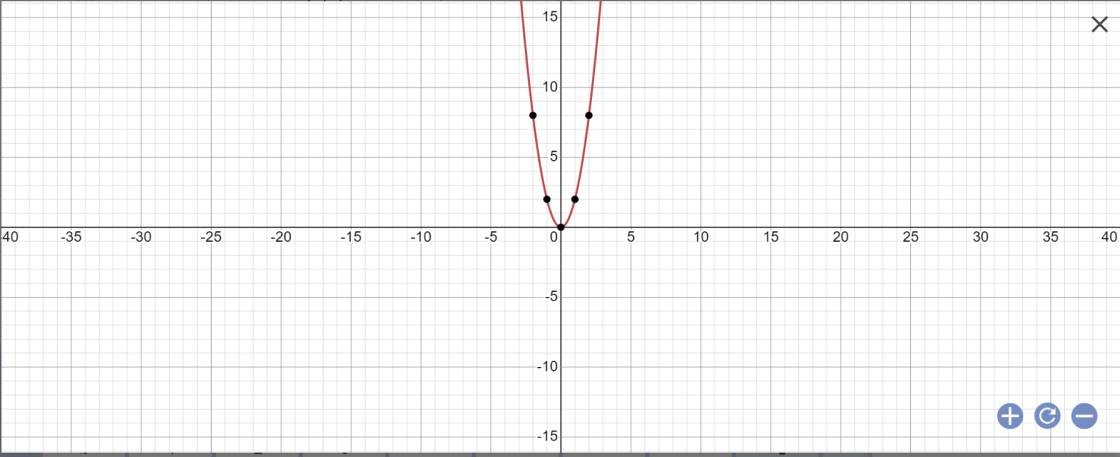
=> Hàm số là y=3x2
b) Các điểm cách đều 2 trục tọa độ có: |x|=|y|
\(\Rightarrow\orbr{\begin{cases}x=y\\x=-y\end{cases}\Leftrightarrow\orbr{\begin{cases}y=3\cdot y^2\\x=3\cdot\left(-y\right)^2\end{cases}\Rightarrow}x=3y^2}\)
<=> y(3y-1)=0
=> \(\orbr{\begin{cases}y=0\\3y-1=0\end{cases}\Leftrightarrow\orbr{\begin{cases}y=0\\y=\frac{1}{3}\end{cases}\Rightarrow}\orbr{\begin{cases}x=0\\x=\frac{-1}{3}\end{cases}}}\)
=> 2 điểm thỏa mãn là: (0;0) và \(\left(\frac{-1}{3};\frac{1}{3}\right)\)
a: Thay x=1 và y=-2 vào (P), ta được:
a*1^2=-2
=>a=-2
b: y=-2x^2