Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a,\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\\ \Rightarrow AEHD\text{ là hcn}\\ \Rightarrow AH=DE\\ b,DI\text{ là tt ứng cạnh huyền }BH\Rightarrow DI=IH\Rightarrow\widehat{IDH}=\widehat{IHD}\\ \text{Mà }AEHD\text{ là hcn }\Rightarrow\widehat{EDH}=\widehat{AHD}\\ \Rightarrow\widehat{IDE}=\widehat{IDH}+\widehat{EDH}=\widehat{IHD}+\widehat{AHD}=\widehat{IHA}=90^0\\ \Rightarrow DI\perp DE\left(1\right)\\ EK\text{ là tt ứng cạnh huyền }CH\Rightarrow EK=KH\Rightarrow\widehat{KEH}=\widehat{KHE}\\ \text{Mà }AEHD\text{ là hcn }\Rightarrow\widehat{AHE}=\widehat{DEH}\\ \Rightarrow\widehat{DEK}=\widehat{DEH}+\widehat{HEK}=\widehat{AHE}+\widehat{KHE}=\widehat{AHK}=90^0\\ \Rightarrow EK\perp DE\left(2\right)\\ \left(1\right)\left(2\right)\Rightarrow DI\text{//}EK\)

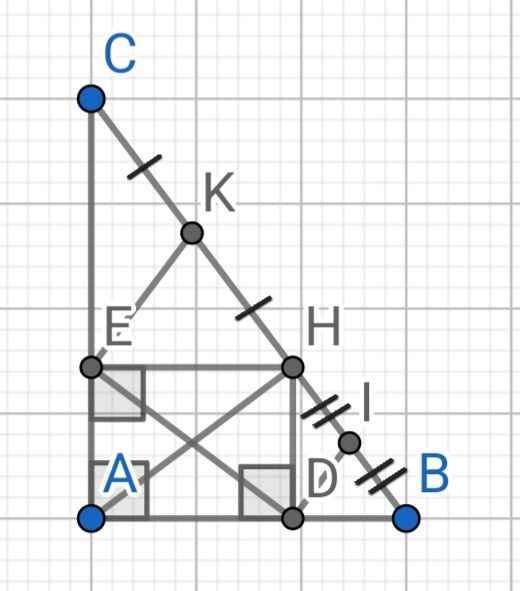 a) Tứ giác ADHE có:
a) Tứ giác ADHE có:
∠AEH = ∠ADH = ∠HAE = 90⁰ (gt)
⇒ ADHE là hình chữ nhật
⇒ AH = DE
b) BHD vuông tại D
I là trung điểm của HB (gt)
⇒ ID = IH = BH : 2
⇒ ∆IDH cân tại I
⇒ ∠IDH = ∠IHD
⇒ ∠HID = 180⁰ - (∠IDH + ∠IHD)
= 180⁰ - 2∠IHD (1)
∆CEH vuông tại E
K là trung điểm HC (gt)
⇒ KE = KC = HC : 2
⇒ ∆KEC cân tại K
⇒ ∠KEC = ∠KCE
⇒ ∠CKE = 180⁰ - (∠KEC + ∠KCE)
= 180⁰ - 2∠KEC (2)
Do HD ⊥ AB (gt)
AC ⊥ AB (gt)
⇒ HD // AC
⇒ ∠IHD = ∠KCE (đồng vị)
⇒ 2∠IHD = 2∠KCE (3)
Từ (1), (2) và (3) ⇒ ∠CKE = ∠HID
Mà ∠CKE và ∠HID là hai góc đồng vị
⇒ DI // KE

cho tam giác ABC vuông tại A đường cao AH ( H thuộc cạnh BC) .gọi D, E theo thứ tự chân đường vuông góc kẻ từ H đến AB và AC .Gọi M, N theo thứ tự là trung điểm của BH và CH .Gọi I là giao điểm của AH và ED
1: cm tam giác DHE là tam giác vuông.Biết AB=3,AC=4, tính
a: bán kính của đường tròn ngoại tiếp tam giác DHE
b: cos ACH
2: cm ED là tiếp tuyến của đường tròn đg kính CH
3: cm I thuộc đg tròn đg kính Mn

a: Xét tứ giác ADHE có
\(\widehat{ADH}=\widehat{AEH}=\widehat{EAD}=90^0\)
Do đó: ADHE là hình chữ nhật
hay AH=DE
giúp e câu b luôn dc ko ạ