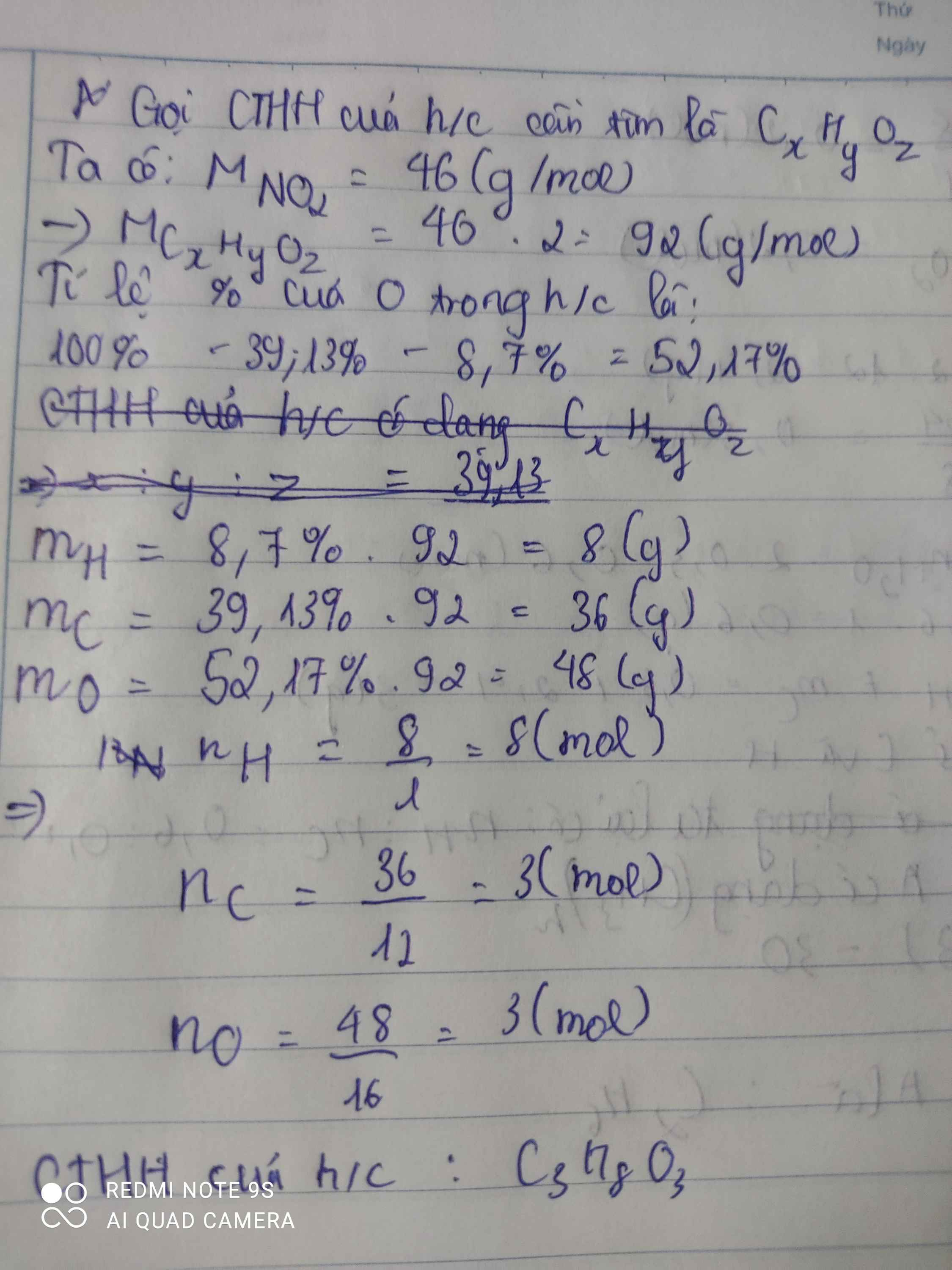Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

CTC: CxHyOz
\(Theo.đề.bài.ta.có:\)
\(x:y:z=\dfrac{76,92}{12}:\dfrac{12,82}{1}:\dfrac{10,26}{16}=6,41:12,82:0,64125\)
\(x:y:z=10:20:1\)
\(Vì.chất.này.có.phân.tử.nhỏ.hơn.\)166g/mol
\(\Rightarrow C_{10}H_{20}O\)
< Cái này ba chỉ mình làm, nếu cách làm chưa được thì bạn thông cảm nhé >

a) \(M_{axit.malic}=\dfrac{67}{0,5}=134\left(g/mol\right)\)
b) \(d_{axit.malic/H_2}=\dfrac{134}{2}=67\)
c) \(m_C:m_H:m_O=35,82\%:4,48\%:59,7\%\)
=> \(n_C:n_H:n_O=\dfrac{35,82}{12}:\dfrac{4,48}{1}:\dfrac{59,7}{16}=4:6:5\)
=> CTPT: (C4H6O5)n
Mà M = 134
=> n = 1
=> CTPT: C4H6O5
d) Gọi số mol (NH2)2CO là a (mol)
=> nH = 4a (mol) (1)
\(n_{C_4H_6O_5}=\dfrac{40,2}{134}=0,3\left(mol\right)\)
=> nH = 1,8 (mol) (2)
(1)(2) => a = 0,45 (mol)
=> \(m_{\left(NH_2\right)_2CO}=0,45.60=27\left(g\right)\)

Gọi CTHH là \(C_xH_yO_z\)
\(\%m_O=100\%-\left(35,82\%+4,48\%\right)=59,7\%\)
\(x:y:z=\dfrac{\%m_C}{12}:\dfrac{\%m_H}{1}:\dfrac{\%m_O}{16}=\dfrac{35,82\%}{12}:\dfrac{4,48\%}{1}:\dfrac{59,7\%}{16}\)
\(=0,02985:0,0448:0,0373125=1:1,5:1,25\)
\(=4:6:5\)
Vậy CTHH là \(C_4H_6O_5\)

Gọi CTHH là CxOy
Ta có: \(\dfrac{m_C}{m_O}=\dfrac{3}{8}\Rightarrow\dfrac{xM_c}{yM_O}=\dfrac{12x}{16y}=\dfrac{3}{8}\Leftrightarrow\dfrac{x}{y}=\dfrac{1}{2}\)
Vậy CTHH: CO2

Gọi CTHH của hợp chất là: \(C_xH_yO_z\)
\(PTHH:2C_xH_yO_z+\dfrac{4x+y-2x}{2}O_2\overset{t^o}{--->}2xCO_2+yH_2O\)
Áp dụng định luật bảo toàn khối lượng, ta có:
\(m_{O_2}=1,08+1,76-1,24=1,6\left(g\right)\)
Ta có: \(m_{O_{\left(hc\right)}}=\dfrac{1,76}{44}.16.2+\dfrac{1,08}{18}.16-1,6=0,64\left(g\right)\)
\(m_{C_{\left(hc\right)}}=m_{C_{\left(CO_2\right)}}=\dfrac{1,76}{44}.12=0,48\left(g\right)\)
\(m_{H_{\left(hc\right)}}=1,24-0,48-0,64=0,12\left(g\right)\)
\(\Rightarrow x:y:z=\dfrac{0,48}{12}:\dfrac{0,12}{1}:\dfrac{0,64}{16}=0,04:0,12:0,04=1:3:1\)
Vậy CTHH của hợp chất là: \(CH_3O\)

chỗ 8,664m=4,448n
<=> \(\frac{m}{n}=\frac{4,448}{8,664}=\frac{1}{2}\)
=> tỉ lệ tối giản là 1:2
chỗ kia mình làm nhầm nha
gọi công thức hợp chất A là CxOy
%C=\(\frac{12x}{12x+16y}.100=45,6\)<=> 6,888x=6,816y
=> \(\frac{x}{y}=\frac{1}{1}\)
=> tỉ lệ tối giản của A là 1:1
tương tự công thức của B : CmOn
%C=\(\frac{12m}{12m+16n}.100=27,8\)
<=> 8,664m=4,448n
<=> \(\frac{m}{n}=\frac{8,664}{4,448}=\frac{2}{1}\)
tỉ lệ tối giản của B là 2:1