Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chiều dòng điện ngược chiều với chiều chuyển động của các electron tức là từ A' đến A ⇒ Áp dụng quy tắc bàn tay trái ⇒ Chiều lực từ thẳng góc với mặt phẳng tờ giấy và từ sau ra trước
→ Đáp án D

a/ Đổi 0,1mm2 = 1. 10-7 m2 . Áp dụng công thức tính điện trở \(R=\rho\frac{l}{S}\) ; thay số và tính \(\Rightarrow\) RAB = 6W
b/ Khi \(AC=\frac{BC}{2}\) \(\Rightarrow\) RAC = \(\frac{1}{3}\).RAB Þ RAC = 2W và có RCB = RAB - RAC = 4W
Xét mạch cầu MN ta có \(\frac{R_1}{R_{AC}}=\frac{R_2}{R_{CB}}=\frac{3}{2}\) nên mạch cầu là cân bằng. Vậy IA = 0
c/ Đặt RAC = x ( ĐK : \(0\le x\le6\Omega\) ) ta có RCB = ( 6 - x )
* Điện trở mạch ngoài gồm ( R1 // RAC ) nối tiếp ( R2 // RCB ) là \(R=\frac{3.x}{3+x}+\frac{6.\left(6-x\right)}{6+\left(6-x\right)}=\)= ?
* Cường độ dòng điện trong mạch chính : \(I=\frac{U}{R}\) ?
* Áp dụng công thức tính HĐT của mạch // có : UAD = RAD . I = \(\frac{3.x}{3+x}.I=\) ?
Và UDB = RDB . I = \(\frac{6.\left(6-x\right)}{12-x}I\) = ?
* Ta có cường độ dòng điện qua R1 ; R2 lần lượt là : I1 = \(\frac{U_{AD}}{R_1}\) = ? và I2 = \(\frac{U_{DB}}{R_2}\) = ?
+ Nếu cực dương của ampe kế gắn vào D thì : I1 = Ia + I2 Þ Ia = I1 - I2 = ? (1)
Thay Ia = 1/3A vào (1) Þ Phương trình bậc 2 theo x, giải PT này được x = 3W ( loại giá trị -18)
+ Nếu cực dương của ampe kế gắn vào C thì : Ia = I2 - I1 = ? (2)
Thay Ia = 1/3A vào (2) Þ Phương trình bậc 2 khác theo x, giải PT này được x = 1,2W ( loại 25,8 vì > 6 )
* Để định vị trí điểm C ta lập tỉ số \(\frac{AC}{CB}=\frac{R_{AC}}{R_{CB}}\) = ? \(\Rightarrow\) AC = 0,3m

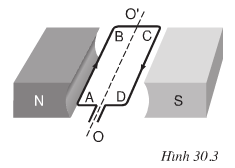
a)Xem hình 30.3b
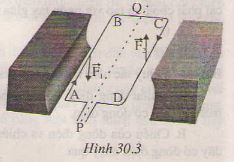
b) Cặp lực \(\overrightarrow{F1}\), \(\overrightarrow{F2}\) làm cho khung dây quay ngược chiều kim đồng hồ.
c)Khung dây quay theo chiều ngược lại khi cặp lực \(\overrightarrow{F1}\), \(\overrightarrow{F2}\) có chiều ngược lại, muốn vậy phải đổi chiều dòng điện trong khung dây hoặc phải đổi chiều từ trường.

Để có được ảnh rõ nét trên màn tức là di chuyển đến TK đến vị trí mà màn chắn hứng được ảnh thật của vật.
Ta có 2 vị trí có thể cho ảnh rõ nét là khi vật cách TK 1 đoạn d hoặc d'=L-d sao cho thỏa mãn: \(\dfrac{1}{d}+\dfrac{1}{d'}=\dfrac{1}{f}\)
Từ công thức suy ra : \(f\left(d+d'\right)=d.d'\)
Giả sử d>d. Ta có: L=d+d' và l=d-d'
=> \(L^2-l^2=\left(d+d'\right)^2-\left(d-d'\right)^2=4d.d'\left(1\right)\)
và : \(4Lf=4\left(d+d'\right)f=4d.d'\left(2\right)\)
Từ (1) và (2) => \(L^2-l^2=4Lf.\)

bài 2
giải
đổi 6kV = 6000V
ta có: \(\frac{U1}{U2}=\frac{N1}{N2}\)
thay số vào ta được: \(\frac{6000}{220}=\frac{12000}{N2}\)
\(\Rightarrow N2=\frac{12000.220}{6000}=440\)(vòng)
vậy......

bài 1:
a/ Quãng đường đi trong 5s đầu: S5 = v0t5 + at52
Quãng đường đi trong 6s:S6 = v0t6 + at62
Quãng đường đi trong giây thứ 6:
S = S6 - S5 = 14 a = 2m/s2
b/ S20 = v0t20 + at202 = 460m
bài 4:
S1 = v0t1 + at12
4.v01 + 8a = 24 (1)
S2 = v01t2 + at22
4.v01 + 8a = 64 (2)
Mà v02 = v1 = v01 + at2 (3)
Giải (1), (2), (3) ta được : v01 = 1m/s, a = 2,5m/s2
2 bài còn lại ko bt lm
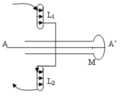

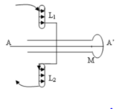

Áp dụng quy tắc nắm tay phải ⇒ Chiều cảm ứng từ có chiều từ L1 đến L2
→ Đáp án A