Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a . thấu kinh phân kỳ
b . Khi không đeo kính,người đó nhìn rõ được vật cách mình 30cm.Vì:
f = -30cm = > f = 20 cm
khi không đeo kính ấy nhìn rõ vật ở gần nhất cách mắt:
f=OC=>OC=30cm.

-Mắt người đó đang bị tật cận thị. Người đó phải đeo kính cận là thấu kính phân kì. Khi đeo kính phù hợp thì ng ấy nhìn rõ vật xa nhất cách mắt ở xa vô cùng. Kính cận thích hợp có tiêu điểm F trùng với điểm cực viễn tức là điểm xa nhất mà mắt có thể nhìn thấy khi không điều tiết. Tiêu cự \(f\)= OF-OF'=50.
(Mình dùng PC nên không vẽ hình đc bạn tự vẽ nhé_ Chúc bạn học tốt nha![]() )
)
Người đó bị tật cận thị . Người đó phải đeo kính cận là thấu kính phân kì . khi đeo kính phù hợp thì người đó có thẻ nhìn rõ vật cách xa . có tiêu cự là 50cm (f= OF-OF'=50).mk xài máy tính nên ko vẽ hình đc mong bạn thông cảm nha ![]()
![]()

Giả sử OA = d = 25cm; OF = f = 50cm; OI = AB;
Vì khi đeo sát mắt một thấu kính hội tụ có tiêu cự 50cm thì mới nhìn rõ vật gần nhất cách mắt 25cm nên ảnh A’B’ của AB qua thấu kính hội tụ phải trùng với điểm cực cận Cc�� của mắt: OCc�� = OA’
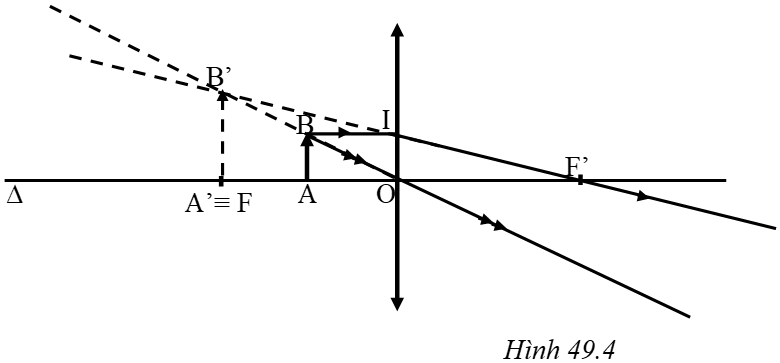
Trên hình 49.4, xét hai cặp tam giác đồng dạng:
ΔA’B’F’ và ΔOIF’; ΔOAB và ΔOA’B’.
Từ hệ thức đồng dạng ta có:
Vì AB = OI (tứ giác BIOA là hình chữ nhật)
→ OCc�� = OA' = OF = 50cm. Như vậy điểm cực cận cách mắt 50cm và khi không đeo kính thì người ấy nhìn rõ vật gần nhất cách mắt 50cm.

Giả sử: \(OA=d=25\left(cm\right)\) ; \(OF=OF'=f=37,5\left(cm\right)\) ; \(OI=AB\)
Ảnh ảo A'B' của AB qua TKHT phải trùng với điểm cực cận của mắt: \(OC_c=OA'\)
Xét tam giác \(OAB\sim\) tam giác \(OA'B'\)
\(\dfrac{AB}{A'B'}=\dfrac{OA}{OA'}=\dfrac{OI}{A'B'}\) ( do AB = OI )
Xét tam giác \(OIF'\sim\) tam giác \(A'B'F'\)
\(\dfrac{OI}{A'B'}=\dfrac{OF'}{A'F'}\) (2)
\(\left(1\right);\left(2\right)\Rightarrow\dfrac{OA}{OA'}=\dfrac{OF'}{A'F'}=\dfrac{OF'}{OA'+OF'}\)
\(\Leftrightarrow\dfrac{25}{OA'}=\dfrac{37,5}{OA'+37,5}\)
\(\Leftrightarrow OA'=75\left(cm\right)\)
Vậy khi không đeo kính thì người đó nhìn rõ được những vật gần nhất cách mắt 75 (cm)


Giả sử OA=25cm; OF=50cm, OI=A′B′, điểm A' trùng C C
Ta có:
A B O I = F A F O = 2505 = 1 2
hay A B A ' B ' = 1 2
Và OA′=2OA=OF=50cm
Ba điểm F,A′ và CC trùng nhau suy ra: OCC=OA′=OF=50cm. Như vậy điểm cực cận cách mắt 50cm và khi không đeo kính thì người ấy nhìn rõ vật gần nhất cách mắt 50cm
Đáp án: C

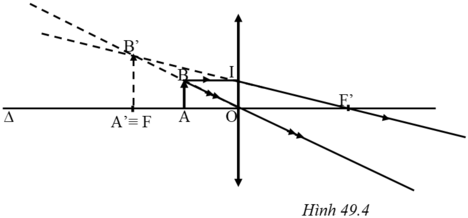
Giả sử OA = d = 25cm; OF = f = 50cm; OI = AB;
Vì khi đeo sát mắt một thấu kính hội tụ có tiêu cự 50cm thì mới nhìn rõ vật gần nhất cách mắt 25cm nên ảnh A’B’ của AB qua thấu kính hội tụ phải trùng với điểm cực cận C c của mắt: O C c = OA’
Trên hình 49.4, xét hai cặp tam giác đồng dạng:
ΔA’B’F’ và ΔOIF’; ΔOAB và ΔOA’B’.
Từ hệ thức đồng dạng ta có:
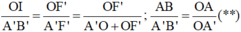
Vì AB = OI (tứ giác BIOA là hình chữ nhật)
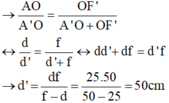
→ O C c = OA' = OF = 50cm. Như vậy điểm cực cận cách mắt 50cm và khi không đeo kính thì người ấy nhìn rõ vật gần nhất cách mắt 50cm.
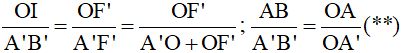
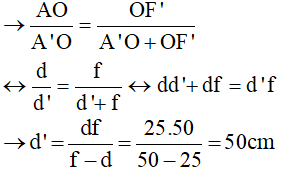
Ta có: \(\dfrac{AB}{A'B'}=\dfrac{OA}{OA'}=\dfrac{OA}{12}\)
\(\Rightarrow\dfrac{AB}{A'B'}=\dfrac{OI}{A'B'}=\dfrac{OF}{OF-OA'}=\dfrac{60}{60-12}=\dfrac{5}{4}\)
\(\Rightarrow\dfrac{OA}{12}=\dfrac{5}{4}\Rightarrow OA=\dfrac{12.5}{4}=15\left(cm\right)\)
Vậy khi đeo kính nhiìn vật AB vị trí đặt vật gần mắt nhất để nhìn rõ là 15cm