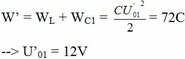Mạch dao động gồm...">
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời. Bài này thì có vẹo gì đâu bạn. \(u=100\sqrt 2\cos(100\pi t)(V)\) \(Z_L=\omega L = 10\Omega\) \(Z_C=\dfrac{1}{\omega C}=20\Omega\) Tổng trở \(Z=\sqrt{r^2+(Z_L-Z_C)^2}=10\sqrt 2 \Omega\) \(\Rightarrow I_o=\dfrac{U_0}{Z}=10A\) \(\tan\varphi=\dfrac{Z_L-Z_C}{R}=-1\Rightarrow \varphi=-\dfrac{\pi}{4}\) Suy ra: \(\varphi=\dfrac{\pi}{4}\) Vậy \(i=10\cos(100\pi t +\dfrac{\pi}{4})\) (A) Có: \(L=CR^2=Cr^2\Rightarrow R^2=r^2=Z_LZ_C,URC=\sqrt{3U}_{Lr}\Leftrightarrow Z^2_{RC}=3Z^2_{Lr}\Leftrightarrow R^2+Z^2_C=3\left(Z^2_L+R^2\right)\) \(\Leftrightarrow-3Z^2_L+Z^2_C=2R^2\) (*) \(R^2=Z_LZ_C\) (**) Từ (*) và (**) có: \(Z_L=\frac{R}{\sqrt{3}};Z_C=\sqrt{3}R\Rightarrow Z=\sqrt{\left(R+r\right)^2Z^2_{LC}}=\frac{4R}{\sqrt{3}}\Rightarrow\cos\phi=\frac{R+r}{Z}=\frac{\sqrt{3}}{2}\approx0,866\) A đúng Đáp án C Phương pháp: Sử dụng định luật bảo toàn năng lượng điện từ
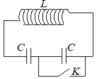
Biểu thức định luật ôm I = E/r Cách giải: +Độ tự cảm của cuộn dây + Cường độ dòng điện cực đại chạy qua cuộn dây: + Hiệu điện thế cực đại trên tụ + Ta có: Chọn A Gọi C là điện dung của mỗi tụ, U0 là điện áp cực đại giữa 2 đầu cuộn dây trước khi đóng K (= điện áp cực đại của bộ tụ) → Điện dung của bộ 2 tụ ghép nối tiếp là: Cb = C/2 Năng lượng ban đầu của mạch: Ngay tại thời điểm Năng lượng của cuộn cảm Năng lượng của tụ điện Ngay sau khi đóng khóa K, một trong hai tụ bị đoản mạch (giả sử tụ C2), phóng năng lượng ra ngoài. Năng lượng của mạch dao động sau khi đóng khoá K là: Hướng dẫn: \(U_{AB}=U_C=2\) (1) \(U_{BC}^2=U_r^2+U_L^2=3\) (2) \(U_{AC}^2=U_r^2+(U_L-U_C)^2=1\) (3) Giải hệ 3 pt trên sẽ tìm đc \(U_r\) và \(U_L\) Chia cho \(I\) sẽ tìm được \(r\) và \(Z_L\) 




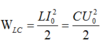
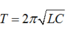
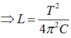
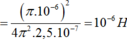
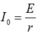
![]()
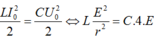
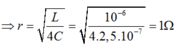

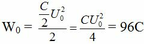
![]() , ta có:
, ta có: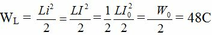
![]()