Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hai tụ ghép // thì Cb = Co + C
Bước sóng: \(\lambda=c.2\pi\sqrt{LC}\)
Ta được hệ PT
\(c.2\pi\sqrt{L\left(Co+\frac{1}{23}.10^{-12}\right)}=0,12\)
\(c.2\pi\sqrt{L\left(Co+0,5.10^{-12}\right)}=0,3\)
Bạn giải hệ PT này và tìm L nhé.

Bước sóng mà mạch thu được λ = 2πc√(LC) = 596m.
Chọn đáp án B

\(\lambda_{max}\le\lambda\le\lambda_{min}\Leftrightarrow c.2\pi\sqrt{L_{min}.C_{min}}\le\lambda c.2\pi\sqrt{L_{max}C_{max}}\)
\(\Leftrightarrow18,8m\le\lambda\le421,5m\)
Đáp án B

Khi tăng điện dung nên 2,5 lần thì dung kháng giảm 2,5 lần. Cường độ dòng trễ pha hơn hiệu điện thế \(\pi\text{/}4\) nên
\(Z_L-\frac{Z_C}{2,5}=R\)
Trường hợp đầu tiên thì thay đổi C để hiệu điện thế trên C cực đại thì
\(Z_LZ_C=R^2+Z^2_L\)
\(Z_LZ_C=\left(Z_L-\frac{Z_C}{2,5}\right)^2+Z^2_L\)
Giải phương trình bậc 2 ta được
\(Z_C=\frac{5}{4}Z_L\) hoặc \(Z_C=10Z_L\) (loại vì Zl-Zc/2.5=R<0)
\(R=\frac{Z_L}{2}\)
Vẽ giản đồ vecto ta được \(U\) vuông góc với \(U_{RL}\) còn \(U_C\) ứng với cạch huyền
Góc hợp bởi U và I bằng với góc hợp bởi \(U_L\) và \(U_{LR}\)
\(\tan\alpha=\frac{R}{Z_L}=0,5\)
\(\sin\alpha=1\text{/}\sqrt{5}\)
\(U=U_C\sin\alpha=100V\)
\(U_o=U\sqrt{2}=100\sqrt{2}V\)
chọn C

- Ta có:
+ Khi L = L1; C = C1 thì:
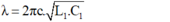
+ Khi L = 3L1; C = C2 thì:
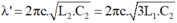
- Vì λ' = 2λ:
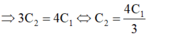
- Khi điều chỉnh cho L = 2L1; C = C1 + 2C2 = 11C1/3 thì mạch thu được bước sóng là:
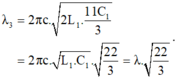

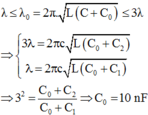
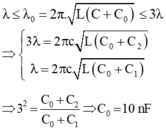
Bước sóng mà mạch thu được
Đáp án B