K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
12 tháng 5 2022
\(\Leftrightarrow\dfrac{1}{3}+\dfrac{1}{6}+...+\dfrac{1}{x\left(x+1\right):2}=\dfrac{1991}{1993}\)
\(\Leftrightarrow\dfrac{2}{6}+\dfrac{2}{12}+...+\dfrac{2}{x\left(x+1\right)}=\dfrac{1991}{1993}\)
\(\Leftrightarrow2\left(\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{x}-\dfrac{1}{x+1}\right)=\dfrac{1991}{1993}\)
\(\Leftrightarrow\dfrac{1}{2}-\dfrac{1}{x+1}=\dfrac{1991}{3986}\)
=>1/x+1=1/1993
=>x+1=1993
hay x=1992
18 tháng 8 2020
\(2\left(1+\frac{1}{3}+\frac{1}{2.3}+\frac{1}{3.4}+......+\frac{1}{x\left(x+1\right)}\right)=\frac{3980}{1991}\)
\(1+\frac{1}{3}+\frac{3-2}{2.3}+\frac{4-3}{3.4}+......+\frac{x+1-x}{x\left(x+1\right)}=\frac{1990}{1991}\)
\(1+\frac{1}{3}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+......+\frac{1}{x}-\frac{1}{x-1}=\frac{1990}{1991}\)
\(1+\frac{1}{3}+\frac{1}{2}-\frac{1}{x-1}=\frac{1990}{1991}\)
\(\frac{1}{x-1}=\frac{11}{6}-\frac{1990}{1991}=\frac{9961}{11946}\)
\(x-1=\frac{11946}{9961}\Rightarrow x=\frac{21907}{9961}\)
16 tháng 4 2017
a)\(\left(-x-\dfrac{1}{9}\right)^2=\dfrac{4}{9}\)
\(\Rightarrow\left(-x-\dfrac{1}{9}\right)^2=\left(\dfrac{2}{3}\right)^2=\left(-\dfrac{2}{3}\right)^2\)
*)Xét \(\left(-x-\dfrac{1}{9}\right)^2=\left(\dfrac{2}{3}\right)^2\)
\(\Rightarrow-x-\dfrac{1}{9}=\dfrac{2}{3}\Rightarrow-x=\dfrac{7}{9}\Rightarrow x=-\dfrac{7}{9}\)
*)Xét \(\left(-x-\dfrac{1}{9}\right)^2=\left(-\dfrac{2}{3}\right)^2\)
\(\Rightarrow-x-\dfrac{1}{9}=-\dfrac{2}{3}\Rightarrow-x=-\dfrac{5}{9}\Rightarrow x=\dfrac{5}{9}\)
b)\(1+\dfrac{1}{3}+\dfrac{1}{6}+\dfrac{1}{10}+...+\dfrac{1}{\dfrac{x\left(x+1\right)}{2}}=1\dfrac{1991}{1993}\)
\(\Rightarrow\dfrac{1}{3}+\dfrac{1}{6}+\dfrac{1}{10}+...+\dfrac{1}{\dfrac{x\left(x+1\right)}{2}}=\dfrac{1991}{1993}\)
\(\Rightarrow\dfrac{2}{6}+\dfrac{2}{12}+\dfrac{2}{20}+...+\dfrac{2}{x\left(x+1\right)}=\dfrac{1991}{1993}\)
\(\Rightarrow\dfrac{2}{2\cdot3}+\dfrac{2}{3\cdot4}+\dfrac{2}{4\cdot5}+...+\dfrac{2}{x\left(x+1\right)}=\dfrac{1991}{1993}\)
\(\Rightarrow2\left(\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{x\left(x+1\right)}\right)=\dfrac{1991}{1993}\)
\(\Rightarrow\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{x\left(x+1\right)}=\dfrac{1991}{3986}\)
\(\Rightarrow\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{x}-\dfrac{1}{x+1}=\dfrac{1991}{3986}\)
\(\Rightarrow\dfrac{1}{2}-\dfrac{1}{x+1}=\dfrac{1991}{3986}\)\(\Rightarrow\dfrac{1}{x+1}=\dfrac{1}{1993}\)
\(\Rightarrow x+1=1993\Rightarrow x=1992\)
28 tháng 7 2017
a) Xét:
\(a>b\)
\(\Rightarrow\dfrac{a}{b}>1\Rightarrow\dfrac{a+m}{b+m}>1\Rightarrow\dfrac{a}{b}>\dfrac{a+m}{a+m}\)
\(a< b\)
\(\Rightarrow\dfrac{a}{b}< 1\Rightarrow\dfrac{a+m}{b+m}< 1\Rightarrow\dfrac{a}{b}< \dfrac{a+m}{b+m}\)
\(a=b\)
\(\Rightarrow\dfrac{a}{b}=1\Rightarrow\dfrac{a+m}{b+m}=1\Rightarrow\dfrac{a}{b}=\dfrac{a+m}{b+m}=1\)
Mk chỉ áp dụng tính 1 câu,câu sau làm tương tự
b)
Ta có:
\(\dfrac{a}{b}< 1\Rightarrow\dfrac{a+m}{b+m}< 1\left(m\in N\right)\)
\(B=\dfrac{10^{1993}+1}{10^{1992}+1}< 1\)
\(B< \dfrac{10^{1993}+1+9}{10^{1992}+1+9}\Rightarrow B< \dfrac{10^{1993}+10}{10^{1992}+10}\Rightarrow B< \dfrac{10\left(10^{1992}+1\right)}{10\left(10^{1991}+1\right)}\Rightarrow B< \dfrac{10^{1992}+1}{10^{1991}+1}=A\)
\(B< A\)
@@ ~ học tốt ~
Q
10 tháng 4 2017
a)
<=> (1/3)[3/(5.8) + 3/(8.11) + ... + 3/[x(x+3)] = 101/1540
<=> (1/3)[(1/5 - 1/8) + (1/8 - 1/11) + ... + 1/x - 1/(x+3)] = 101/1540
<=> (1/3)[1/5 - 1/(x+3)] = 101/1540
<=> 1/5 - 1/(x+3) = 303/1540
<=> 1/(x+3) = 1/5 - 303/1540 = 5/1540 = 1/308
<=> x = 305
b)
10 tháng 4 2017
a)\(\dfrac{1}{5.8}+\dfrac{1}{8.11}+\dfrac{1}{11.14}+...+\dfrac{1}{x.\left(x+3\right)}=\dfrac{101}{1540}\)
\(\dfrac{1.3}{5.8}+\dfrac{1.3}{8.11}+\dfrac{1.3}{11.14}+...+\dfrac{1.3}{x.\left(x+3\right)}=\dfrac{101.3}{1540}\)
\(\dfrac{3}{5.8}+\dfrac{3}{8.11}+\dfrac{3}{11.14}+...+\dfrac{3}{x.\left(x+3\right)}=\dfrac{303}{1540}\)
\(\dfrac{1}{5}-\dfrac{1}{8}+\dfrac{1}{8}-\dfrac{1}{11}+\dfrac{1}{11}-\dfrac{1}{14}+...+\dfrac{1}{x}-\dfrac{1}{x+3}=\dfrac{303}{1540}\)
\(\dfrac{1}{5}-\dfrac{1}{x+3}=\dfrac{303}{1540}\)
\(\dfrac{1}{x+3}=\dfrac{1}{5}-\dfrac{303}{1540}\)
\(\dfrac{1}{x+3}=\dfrac{1}{308}\)
308.1 = (x + 3).1
308 = x + 3
x = 308 - 3
x = 305
CX
2
UM
25 tháng 10 2015
M= 20217.20217.20217.20217......20217-20213.20213.20213.......20213
M= (20217.20217).(20217.20217).(20217.20217).......(20217.20217)-(20213.20213.20213.20213).(20213.20213.20213.20213)...................(20213.20213.20213.20213)
M= .....9.....9......9.....9.............9.......7-....1....1....1....1...1...........1......3....3......3
M= ....3-.....7
M=.....6
=> đề sai
I
2
11 tháng 6 2016
Ta có: B= 3 + 33 + 35 + ... + 31991= (3 + 33 + 35) + (37+ 39 + 311 ) + ... + (31987 + 31989 + 31991).
= 3 x (1 + 32 + 34) + 37 x (1 + 32 + 34) + ... + 31987 x (1 + 32 + 34).
= 3 x 91 + 37 x 91 + ... + 31987 x 91= 3 x 7 x 13 + 37 x 7 x 13 + ... + 31987 x 7 x 13.
= 13 x ( 3 x 7 + 37 x 7 + ... + 31987 x 7).
Vì B = 13 x ( 3 x 7 + 37 x 7 + ... + 31987 x 7) nên B chia hết cho 13.
B= (3 + 33 + 35 + 37) + ... + (31985 + 31987 + 31989 + 31991).
= 3 x (1 + 32 + 34 + 36) + ... + 31985 x (1 + 32 + 34 + 36).
= 3 x 820 + ... + 31985 x 820= 3 x 20 x 41 + ... + 31985 x 20 x 41.
= 41 x ( 3 x 20 + .. + 31985 x 20)
Vì B =41 x ( 3 x 20 + .. + 31985 x 20) nên B chia hết cho 41.
KC
11 tháng 6 2016
Ta có: B= 3 + 33 + 35 + ... + 31991= (3 + 33 + 35) + (37+ 39 + 311 ) + ... + (31987 + 31989 + 31991).
= 3 x (1 + 32 + 34) + 37 x (1 + 32 + 34) + ... + 31987 x (1 + 32 + 34).
= 3 x 91 + 37 x 91 + ... + 31987 x 91= 3 x 7 x 13 + 37 x 7 x 13 + ... + 31987 x 7 x 13.
= 13 x ( 3 x 7 + 37 x 7 + ... + 31987 x 7).
Vì B = 13 x ( 3 x 7 + 37 x 7 + ... + 31987 x 7) nên B chia hết cho 13.
B= (3 + 33 + 35 + 37) + ... + (31985 + 31987 + 31989 + 31991).
= 3 x (1 + 32 + 34 + 36) + ... + 31985 x (1 + 32 + 34 + 36).
= 3 x 820 + ... + 31985 x 820= 3 x 20 x 41 + ... + 31985 x 20 x 41.
= 41 x ( 3 x 20 + .. + 31985 x 20)
Vì B =41 x ( 3 x 20 + .. + 31985 x 20) nên B chia hết cho 41.
CX
1
NT
31 tháng 10 2015
Xét số 202171993 ta thấy 202171993=202174k+1=>202171993 có tận cùng là 7
Xét số 202131991 ta thấy 202131991=202134k+3=>202131991 có tận cùng là 7
Mà ......7-.......7 có tận cùng là 0 =>M chia hết cho 5=>M có dạng 5k
=>ĐPCM
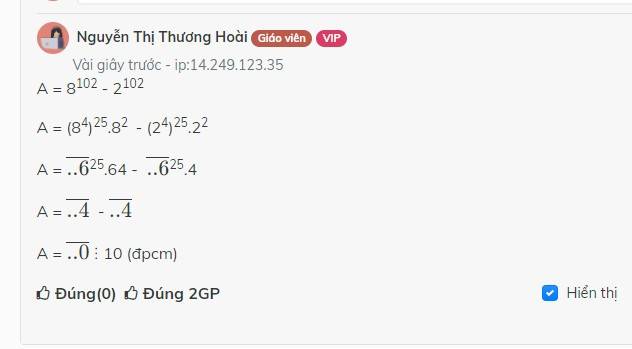
m : 1 - m x 1 = m - m = 0
suy ra : 0 : ( m x 1991 + m + 1 ) = 0
nhấn đúng cho mình nha