K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

11 tháng 2 2017
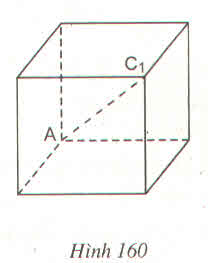
We can easily prove that : \(AC'^2=2.A'B'^2\Rightarrow3=2.AB^2\Rightarrow AB=\sqrt{\frac{3}{2}}\) ( AB > 0 )
We also have \(AB\)is the side of this cube. So its total surface area is \(AB.AB.6=\frac{3}{2}.6=9\)

23 tháng 4 2017
A B C D A' B' C' D'
xét hình vuông ABCD có:
\(CD^2+AD^2=AC^2\Leftrightarrow2AD^2=AC^2\Leftrightarrow AD^2=\dfrac{AC^2}{4}=\dfrac{\left(4\sqrt{2}\right)^2}{4}=\dfrac{16\cdot2}{2}=16\\ \Rightarrow AD=\sqrt{16}=4\left(cm\right)\)
ta có:
diện tích xung quanh của hình lập phương= \(4\cdot AD^2=4\cdot4^2=64\left(cm^2\right)\)
diện tích toàn phần =\(6\cdot AD^2=6\cdot4^2=96\left(cm^2\right)\)
thể tích =\(AD^3=4^3=64\left(cm^3\right)\)