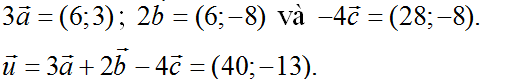Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(h\overrightarrow{a}+k\overrightarrow{b}=\left(2h;4h\right)+\left(3k;-5k\right)=\left(2h+3k;4h-5k\right)\)
\(\overrightarrow{u}=h\overrightarrow{a}+k\overrightarrow{b}\Leftrightarrow\left\{{}\begin{matrix}2h+3k=8\\4h-5k=-6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}h=1\\k=2\end{matrix}\right.\)

a) \(\overrightarrow{u}=3\overrightarrow{a}+2\overrightarrow{b}-4\overrightarrow{c}=3\left(2;1\right)+2\left(3;-4\right)-4\left(-7;2\right)\)
\(=\left(6;3\right)+\left(6;-8\right)-\left(-28;8\right)\)
\(=\left(6+6+28;3-8-8\right)=\left(40;-13\right)\).
b) \(\overrightarrow{x}+\overrightarrow{a}=\overrightarrow{b}-\overrightarrow{c}\Leftrightarrow\overrightarrow{x}=\overrightarrow{b}-\overrightarrow{c}-\overrightarrow{a}\)
\(\Leftrightarrow\overrightarrow{x}=\left(3;-4\right)-\left(-7;2\right)-\left(2;1\right)\)
\(\Leftrightarrow\overrightarrow{x}=\left(3+7-2;-4-2-1\right)\)
\(\Leftrightarrow\overrightarrow{x}=\left(8;-7\right)\).
c) Có \(\overrightarrow{c}\left(-7;2\right)=k\overrightarrow{a}+h\overrightarrow{b}=k\left(2;1\right)+h\left(3;-4\right)\)
\(=\left(2k+3h;k-4h\right)\).
Từ đó suy ra: \(\left\{{}\begin{matrix}2k+3h=-7\\k-4h=2\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}k=-2\\h=-1\end{matrix}\right.\).

\(\left(\overrightarrow{a}+\overrightarrow{b}\right)^2=\left(\overrightarrow{a}+\overrightarrow{b}\right)\left(\overrightarrow{a}+\overrightarrow{b}\right)\)\(=\left|\overrightarrow{a}\right|^2+\left|\overrightarrow{b}\right|^2+2\overrightarrow{a}\overrightarrow{b}\).
\(\left(\overrightarrow{a}-\overrightarrow{b}\right)^2=\left(\overrightarrow{a}-\overrightarrow{b}\right)\left(\overrightarrow{a}-\overrightarrow{b}\right)\)\(=\left|\overrightarrow{a}\right|^2+\left|\overrightarrow{b}\right|^2-2\overrightarrow{a}\overrightarrow{b}\).
\(\left(\overrightarrow{a}-\overrightarrow{b}\right)\left(\overrightarrow{a}+\overrightarrow{b}\right)=\left|\overrightarrow{a}\right|^2+\overrightarrow{a}\overrightarrow{b}-\overrightarrow{a}\overrightarrow{b}+\left|\overrightarrow{b}\right|^2\)\(=\left|\overrightarrow{a}\right|^2-\left|\overrightarrow{b}\right|^2\).

Hok nhanh phết, chưa j đã đến phần toạ độ vecto r
1/ \(\overrightarrow{MB}=\left(x_B-x_M;y_B-y_M\right)=\left(2-x_M;3-y_M\right)\)
\(\Rightarrow2\overrightarrow{MB}=\left(4-2x_M;6-2y_M\right)\)
\(\overrightarrow{3MC}=\left(3x_C-3x_M;3y_C-3y_M\right)=\left(-3-3x_M;6-3y_M\right)\)
\(\Rightarrow2\overrightarrow{MB}+3\overrightarrow{MC}=\left(4-2x_M-3-3x_M;6-2y_M+6-3y_M\right)=0\)
\(\Leftrightarrow\left(1-5x_M;12-5y_M\right)=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}1-5x_M=0\\12-5y_M=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_M=\frac{1}{5}\\y_M=\frac{12}{5}\end{matrix}\right.\Rightarrow M\left(\frac{1}{5};\frac{12}{5}\right)\)
2/ \(\overrightarrow{m}=2\left(1;2\right)+3\left(3;4\right)=\left(2+9;4+12\right)=\left(11;16\right)\)
3/ \(\overrightarrow{AB}=\left(x_B-x_A;y_B-y_A\right)=\left(-5-3;4+2\right)=\left(-8;6\right)\)
\(\overrightarrow{AC}=\left(x_C-x_A;y_C-y_A\right)=\left(\frac{1}{3}-3;0+2\right)=\left(-\frac{8}{3};2\right)\)
\(\Rightarrow x=\frac{\overrightarrow{AB}}{\overrightarrow{AC}}=\frac{\left(-8;6\right)}{\left(-\frac{8}{3};2\right)}=3\)
Câu 4 tương tự
Câu 5 vt lại đề bài nhé bn, nghe nó vô lý sao á, m,n ở đâu ra vậy, cả A,B,C nx

\(\overrightarrow{MC}=\left(1-k\right)\overrightarrow{MA}+k\overrightarrow{MB}\)
\(\Leftrightarrow\overrightarrow{MC}-\overrightarrow{MA}=k\left(\overrightarrow{MB}-\overrightarrow{MA}\right)\)
\(\Leftrightarrow\overrightarrow{AC}=k\overrightarrow{AB}\)
\(\Rightarrow\)A,B,C thẳng hàng (đpcm)