Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B
Mặt cầu (S): (x-1)²+ (y-2)²+ (z-3)²=9 có tâm I (1;2;3), bán kính R=3.
IA = √6 < R nên A nằm trong mặt cầu.
Gọi r là bán kính đường tròn thiết diện, ta có ![]()
Trong đó h là khoảng cách từ I đến (P).
Diện tích thiết diện là
![]()
Vậy diện tích hình tròn (C) đạt nhỏ nhất khi h = IA. Khi đó ![]() là véc tơ pháp tuyến của (P).
là véc tơ pháp tuyến của (P).
Phương trình mặt phẳng (P) là 1 (x-0)+2 (y-0)+ (z-2)=0 ó x + 2y + z – 2 = 0

Đáp án B
Phương trình của mặt phẳng (P) là 3(x-0)+2(y-0)+1(z-0)=0<=> 3x+2y+z=0.

Đáp án A.
Gọi:
![]()
Phương trình mặt phẳng (P) có dạng:

Vì M là trực tâm của tam giác ABC nên
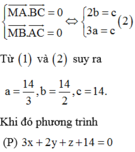

Hình chiếu của điểm A(2; 3; 4) lên các trục Ox, Oy, Oz lần lượt là B(2; 0; 0), C(0; 3; 0), D(0; 0 ; 4). Mặt phẳng ( α ) đi qua ba điểm B, C, D nên
( α ) có phương trình theo đoạn chắn là:
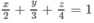
hay 6x + 4y + 3z – 12 = 0

Đáp án C
Gợi A’, B’ C’ hình chiếu của A lên Ox, Oy, Oz. Ta có:
A'(5;0;0), B'(0;4;0), C(0;0;3) => PT ( α ) : x 5 + y 4 + z 3 = 1

Đáp án D
Với điểm A(2;-3;4). Hình chiếu của A trên 3 trục tọa độ lần lượt là:
B(2; 0; 0); C( 0; -3; 0) và D( 0; 0; 4).
Phương trình mặt phẳng (BCD) là:
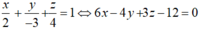

Đáp án B
Xét ( S ) : x 1 2 + y - 2 2 + z - 3 2 = 16 có tâm I(1;2;3), bán kính R = 4
Gọi O là hình chiếu của I trên (P).
![]()
Khi và chỉ khi IO ≡ IHvới H là hình chiếu của I trên AB.
I H → là véc tơ pháp tuyến của mp (P) mà IA = IB => H là trung điểm của AB
![]()
![]()
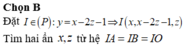
Gọi I(a;b;c) và r lần lượt là tâm và bán kính mặt cầu (S).
Phương trình mặt cầu (S) có dạng: (x-a)2+(y-b)2+(z-c)2=r2.
a) (S) đi qua các điểm C(2;-4;3), (2;0;0), (0;-4;0) và (0;0;3).
Ta có hệ phương trình:
\(\left\{{}\begin{matrix}\left(2-a\right)^2+\left(-4-b\right)^2+\left(3-c\right)^2=r^2\\\left(2-a\right)^2+b^2+c^2=r^2\\a^2+\left(-4-b\right)^2+c^2=r^2\\a^2+b^2+\left(3-c\right)^2=r^2\end{matrix}\right.\) \(\Rightarrow\) a=1, b=-2, c=3/2, r2=29/4.
Phương trình cần tìm là: (S): (x-1)2+(y+2)2+(z-3/2)2=29/4.
b) (S) đi qua các điểm C(2;-4;3), (2;-4;0), (2;0;3) và (0;-4;3).
Ta có hệ phương trình:
\(\left\{{}\begin{matrix}\left(2-a\right)^2+\left(-4-b\right)^2+\left(3-c\right)^2=r^2\\\left(2-a\right)^2+\left(-4-b\right)^2+c^2=r^2\\a^2+\left(-4-b\right)^2+\left(3-c\right)^2=r^2\\\left(2-a\right)^2+b^2+\left(3-c\right)^2=r^2\end{matrix}\right.\) \(\Rightarrow\) a=1, b=-2, c=3/2, r2=29/4.
Phương trình cần tìm là: (S): (x-1)2+(y+2)2+(z-3/2)2=29/4.