Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do tâm sai của ( E) là 1/2 nên
![]()
mà Elip qua điểm (6;0) nên a= 6
=> c= 3 => b2= a2- c2= 36- 9= 27
Vậy
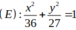
Chọn A.

Đường thẳng Δ song song với d ⇒ Δ: x + y + c = 0, (c ≠ 0)
Vì Δ đi qua A ⇒ 3 + 0 + c = 0 ⇒ c = -3(tm)
Vậy đường thẳng Δ có dạng: x+y-3=0
Vì đường tròn có tâm I thuộc d nên I(a;-a)
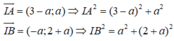
Vì đường tròn đi qua A, B nên I A 2 = I B 2 ⇒ (3 - a ) 2 + a 2 = a 2 + (2 + a ) 2 ⇔ (3 - a ) 2 = (2 + a ) 2
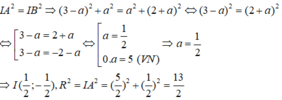
Vậy phương trình đường tròn có dạng:
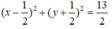
Ta có:
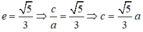
Giả sử elip (E) có dạng:
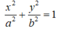
Vì (E) đi qua B nên:
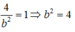
Mà
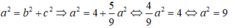
Vậy phương trình chính tắc của elip (E) là:
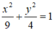

Gọi phương trình chính tắc elip cần tìm là
![]() .
.
Do elip đi qua
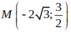 ,
, 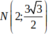
nên ta có hệ
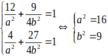
Vậy elip cần tìm là
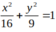
Chọn C.

\(F_1F_2=2c=2\sqrt{5}\)
\(\Rightarrow c=\dfrac{2\sqrt{5}}{2}=\sqrt{5}\)
\(\left(E\right)\) qua \(\left(5;0\right)\Rightarrow a=5\)
Ta có : \(b=\sqrt{a^2-c^2}\)
\(\Rightarrow b^2=a^2-c^2\)
\(\Rightarrow b^2=5^2-\sqrt{5}^2\)
\(\Rightarrow b^2=25-5=20\)
Vậy \(PTCT\left(E\right):\dfrac{x^2}{25}+\dfrac{y^2}{20}=1\)

Gọi Elip cần tìm có dạng : (E) : 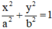
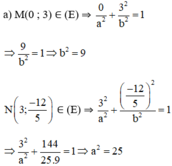
Vậy phương trình chính tắc của elip: 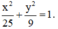

Đáp án A
Ta có tâm sai 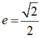
khoảng cách giữa hai đường chuẩn là:
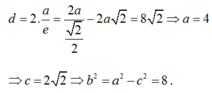
Suy ra phương trình elip là:
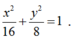

1: (E): x^2/a^2+y^2/b^2=1
Thay x=0 và y=3 vào (E), ta được:
3^2/b^2=1
=>b^2=9
=>b=3
F2(5;0)
=>c=5
=>\(\sqrt{a^2-9}=5\)
=>a^2-9=25
=>a^2=34
=>\(a=\sqrt{34}\)
=>x^2/34+y^2/9=1
2: Thay x=7 và y=0 vào (E), ta được:
7^2/a^2+0^2/b^2=0
=>a^2=49
=>a=7
Thay x=0 và y=3 vào (E), ta được:
0^2/a^2+3^2/b^2=1
=>b^2=9
=>b=3
=>(E): x^2/49+y^2/9=1
3: Thay x=0 và y=1 vào (E), ta được:
1/y^2=1
=>y=1
=>(E): x^2/a^2+y^2/1=1
Thay x=1 và y=căn 3/2 vào (E), ta được:
1^2/a^2+3/4=1
=>1/a^2=1/4
=>a^2=4
=>a=2
=>(E); x^2/4+y^2/1=1

a) Phương trình đường tròn (C) có tâm \(I\left( { - 4;2} \right)\) và bán kính \(R = 3\) là: \({\left( {x + 4} \right)^2} + {\left( {y - 2} \right)^2} = 9\).
b) Bán kính đường tròn là: \(R = PE = \sqrt {{{\left( {1 - 3} \right)}^2} + {{\left( {4 + 2} \right)}^2}} = \sqrt {40} \)
Phương trình đường tròn là: \({\left( {x - 3} \right)^2} + {\left( {y + 2} \right)^2} = 40\).
c) Bán kính đường tròn là: \(R = \frac{{\left| {3.5 + 4.\left( { - 1} \right) - 1} \right|}}{{\sqrt {{3^2} + {4^2}} }} = \frac{{10}}{5} = 2\)
Phương trình đường tròn là: \({\left( {x - 5} \right)^2} + {\left( {y + 1} \right)^2} = 4\)
d) Giả sử tâm đường tròn là điểm \(I\left( {a;b} \right)\). Ta có: \(IA = IB = ID \Leftrightarrow I{A^2} = I{B^2} = I{D^2}\)
Vì \(I{A^2} = I{B^2},I{B^2} = I{D^2}\) nên: \(\left\{ \begin{array}{l}{\left( { - 3 - a} \right)^2} + {\left( {2 - b} \right)^2} = {\left( { - 2 - a} \right)^2} + {\left( { - 5 - b} \right)^2}\\{\left( { - 2 - a} \right)^2} + {\left( { - 5 - b} \right)^2} = {\left( {5 - a} \right)^2} + {\left( {2 - b} \right)^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = - 1\end{array} \right.\)
=> \(I\left( {1; - 1} \right)\) và \(R = IA = \sqrt {{{\left( 4 \right)}^2} + {{\left( { - 3} \right)}^2}} = 5\)
Vậy phương trình đường tròn đi qua 3 điểm A,B, D là: \({\left( {x - 1} \right)^2} + {\left( {y + 1} \right)^2} = 25\)

Gọi pt (E) có dạng \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)
\(e=\frac{c}{a}=\frac{2}{3}\Rightarrow c=\frac{2a}{3}\Rightarrow c^2=\frac{4a^2}{9}\)
\(\Rightarrow b^2=a^2-c^2=\frac{5a^2}{9}\)
Pt (E) có dạng: \(\frac{x^2}{a^2}+\frac{\frac{9}{5}y^2}{a^2}=1\Leftrightarrow a^2=x^2+\frac{9}{5}y^2\)
Thay tọa độ M vào ta được:
\(a^2=2^2+\frac{9}{5}\left(\frac{5}{2}\right)^2=\frac{61}{4}\Rightarrow b^2=\frac{305}{36}\)
Pt (E): \(\frac{x^2}{\frac{61}{4}}+\frac{y^2}{\frac{305}{36}}=1\)