Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi x (đồng) là giá tiền của 1kg sắt φ 8, y (đồng) là khoản chi phí làm trần của tầng một. Điều kiện: x > 0, y > 0
Khi đó giá tiền của 1kg sắt là φ 18 là 22x (đồng)
Vì tầng một dùng 30 cây sắt φ 18 và 350kg sắt φ 8 hết y đồng nên ta có: 30.22x + 350x = y
Vì tầng hai dùng 20 cây sắt φ 18 và 250kg sắt φ 8 hết ít hơn tầng một 1440000 đồng nên ta có: 20.22x + 250x = y – 1440000
Ta có hệ phương trình:
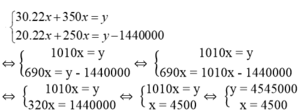
Giá trị của x và y thỏa điều kiện bài toán.
Vậy giá 1kg sắt φ 8 là 4500 đồng,
giá 1 cây sắt φ 18 là 4500.22 = 99000 đồng.

.
\(A\cap B\ne\varnothing\)khi \(\hept{\begin{cases}b\le a+2\\b+1\ge a\end{cases}\Leftrightarrow\hept{\begin{cases}b-a\le2\\b-a\ge-1\end{cases}}}\Leftrightarrow-1\le b-a\le2.\)
a a+2 b+1 b
Ta tìm điều kiện để \(A\cap B=\varnothing\).
Có hai trường hợp :
TH1: \(a+2< b.\)
TH2: \(b+1< a.\)
Để hai trường hợp đều không xảy ra thì \(\hept{\begin{cases}a+2\ge b\\a\le b+1\end{cases}\Rightarrow\hept{\begin{cases}a\ge b-2\\a\le b+1\end{cases}\Rightarrow}b-2\le a\le b+1.}\)

Vì A khác rỗng
=> Tồn tại số a \(\in\)A => 1 - a \(\in\)A và 1/a \(\in\)A
=> \(\frac{1}{1-a}\in A;1-\frac{1}{a}=\frac{a-1}{a}\in A\)
=> \(1-\frac{1}{1-a}\in A;\frac{a}{a-1}=1-\frac{1}{1-a}\in A\)
Mà A chỉ có chứa tối đa 5 phần tử
=> \(a=1-\frac{1}{1-a}\Leftrightarrow a=\frac{a}{a-1}\Leftrightarrow\orbr{\begin{cases}a=2\\a=0\left(loai\right)\end{cases}}\Leftrightarrow a=2\)
Vậy tập A = { 2; -1; 1/2}

Đáp án C
giải
Chuyển vế sau đó bình phương lên
\(\sqrt{x+4}=2-\sqrt{x-1}\)
\(\Leftrightarrow\left(\sqrt{x+4}\right)^2=\left(2-\sqrt{x-1}\right)^2\)
Khai triển cái này ra xog sẽ được
\(\sqrt{x-1}=-\frac{1}{4}\) ( Vô lí)
Suy ra ko tồn tại giá trị x thỏa mãn
Hay tập nghiệm là rỗng

=
1111111111111111111111111111111111111111111111111111111111111111111111111111111111111
Cả hai ddeuf bằng nhau
Vì bông nhệ hơn sắt nhưng cùng bằng 1kg
=>1kg bông bằng 1kg sắt

Do tập A có 3 phần tử, theo nguyên lý Dirichlet thì hai tập con bất kì có nhiều hơn 1 phần tử của A đều có chung ít nhất 1 phần tử hay giao của chúng khác rỗng
\(\Rightarrow\) Các tập con của A có giao bằng rỗng khi và chỉ khi chúng có không nhiều hơn 1 phần tử
\(\Rightarrow\) Các tập đó là: \(\varnothing;\left\{a\right\};\left\{b\right\};\left\{c\right\}\)
Có \(C_4^2=6\) cặp thỏa mãn
