Làm tính nhân phân thức: 30 x 3...

K

Khách

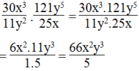
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

PT

Pham Trong Bach

26 tháng 9 2018

Làm tính nhân phân thức: 30 x 3 11 y 2 . 121 y 5 25 x

#Hỏi cộng đồng OLM #Toán lớp 8

1

CM

Cao Minh Tâm

26 tháng 9 2018

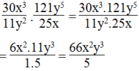
Giải sách bài tập Toán 8 | Giải bài tập Sách bài tập Toán 8

Các câu hỏi dưới đây có thể giống với câu hỏi trên

K

©ⓢ丶κεη春╰‿╯

24 tháng 2 2020 - olm

B3 : a) Làm Tính Nhân : \(\left(4x^3-xy^2+y^3\right)\left(x^2y+2xy^2-2y^3\right)\)b) Phân tích đa thức thành nhân tử :(!) \(2\left(x+y\right)^2-7\left(x+y\right)+5\)(!!) \(\left(x+y+z\right)^2-x^2-y^2-z^2\)c) Tính GTBT : \(x^3-y^3-x^2-y^2-11xy\) biết \(x-y=3\)d)Tìm giá trị biểu thức của a và b để...

#Hỏi cộng đồng OLM #Toán lớp 8

2

KN

Kiệt Nguyễn

24 tháng 2 2020

a)\(\left(4x^3-xy^2+y^3\right)\left(x^2y+2xy^2-2y^3\right)\)

\(=x^2y\left(4x^3-xy^2+y^3\right)+2xy^2\left(4x^3-xy^2+y^3\right)\)

\(-2y^3\left(4x^3-xy^2+y^3\right)\)

\(=4x^5y-x^3y^3+x^2y^4+8x^4y^2-2x^2y^4+2xy^5\)

\(-8x^3y^3+2xy^5-2y^6\)

\(=-2y^6+4x^5y+\left(2xy^5+2xy^5\right)+8x^4y^2+\left(x^2y^4-2x^2y^4\right)\)

\(-\left(x^3y^3+8x^3y^3\right)\)

\(=-2y^6+4x^5y+4xy^5+8x^4y^2-x^2y^4-9x^3y^3\)

KN

Kiệt Nguyễn

24 tháng 2 2020

b)

(!) \(2\left(x+y\right)^2-7\left(x+y\right)+5\)

\(=2\left(x+y\right)^2-2\left(x+y\right)-5\left(x+y\right)+5\)

\(=2\left(x+y\right)\left(x+y-1\right)-5\left(x+y-1\right)\)

\(=\left(2x+2y-5\right)\left(x+y-1\right)\)

(!!) \(\left(x+y+z\right)^2-x^2-y^2-z^2\)

\(=\left(x^2+y^2+z^2+2xy+2yz+2zx\right)-x^2-y^2-z^2\)

\(=2\left(xy+yz+zx\right)\)

N

Name

5 tháng 1 2022

1, Làm tính nhân : 3xy(x^2-2xy+5)

Phân tích đa thức thành nhân tử : x^2+2xy-25+y^2

#Hỏi cộng đồng OLM #Toán lớp 8

2

NL

Nguyễn Lê Phước Thịnh

5 tháng 1 2022

Bài 1:

\(=3x^3y-6x^2y^2+15xy\)

Bài 2:

\(=\left(x+y\right)^2-25=\left(x+y+5\right)\left(x+y-5\right)\)

KS

Kudo Shinichi

5 tháng 1 2022

\(x^2+2xy-25+y^2\\ =\left(x^2+2xy+y^2\right)-5^2\\ =\left(x+y\right)^2-5^2\\ =\left(x+y-5\right)\left(x+y+5\right)\)

N

Name

5 tháng 1 2022

1, Làm tính nhân : 3xy(x^2-2xy+5)

Phân tích đa thức thành nhân tử : x^2+2xy-25+y^2\

2.Tìm xy biết a) 4x^2+20x=0

b ) x(x+3)-3x-9=0

#Hỏi cộng đồng OLM #Toán lớp 8

1

NL

Nguyễn Lê Phước Thịnh

5 tháng 1 2022

Bài 2:

a: =>4x(x+5)=0

=>x=0 hoặc x=-5

b: =>(x+3)(x-3)=0

=>x=-3 hoặc x=3

AK

Akabane Karma

5 tháng 1 2019 - olm

Phân tích các đa thức sau thành nhân...

#Hỏi cộng đồng OLM #Toán lớp 8

3

H

❤ Hoa ❤

5 tháng 1 2019

\(\frac{2}{5}x\left(y-1\right)-\frac{2}{5}y\left(y-1\right)\)

\(=\left(y-1\right)\left[\left(\frac{2}{5}x-\frac{2}{5}y\right)\right]\)

\(=\left(y-1\right)\frac{2}{5}\left(x-y\right)\)

H

❤ Hoa ❤

5 tháng 1 2019

\(\frac{1}{25}x^2-64y^2\)

\(=\left(\frac{1}{5}x\right)^2-8^2\)

\(=\left(\frac{1}{5}x+8\right)\left(\frac{1}{5}x-8\right)\)

NP

Nguyễn Phan Thục Trinh

30 tháng 1 2019 - olm

a/ Phân tính đa thức thành nhân tử: (với hệ số là các số nguyên)

\(x^2+2xy+7x+7y+y^2+10\)

b) Biết xy=11 và \(x^2y+xy^2+x+y=2010.\)Hãy tính \(x^2+y^2\)

#Hỏi cộng đồng OLM #Toán lớp 8

1

NH

Nguyễn Hưng Phát

30 tháng 1 2019

a,\(x^2+2xy+7x+7y+y^2+10=\left(x^2+2xy+y^2\right)+7\left(x+y\right)+10\)

\(=\left(x+y\right)^2+2\left(x+y\right)+5\left(x+y\right)+10\)

\(=\left(x+y\right)\left(x+y+2\right)+5\left(x+y+2\right)\)

\(=\left(x+y+2\right)\left(x+y+5\right)\)

b,\(x^2y+xy^2+x+y=2010\Rightarrow xy\left(x+y\right)+x+y=2010\)

\(\Rightarrow12\left(x+y\right)=2010\Rightarrow x+y=167,5\)

Ta có:\(x^2+y^2=x^2+2xy+y^2-2xy=\left(x+y\right)^2-2xy=\left(167,5\right)^2-2.11=28034,25\)

GD

giang đào phương

18 tháng 6 2021 - olm

phân tích đa thức thành nhân tử

a, \(100x^2-\left(x^2+25\right)^2\)

b, \(\left(x-y+5\right)^2-2\left(x-y+5\right)+1\)

c, \(\left(x^2+4y^2-5\right)^2-16\left(x^2+y^2+2xy+1\right)\)

#Hỏi cộng đồng OLM #Toán lớp 8

1

DD

Đoàn Đức Hà

Giáo viên

19 tháng 6 2021

a) \(100x^2-\left(x^2+25\right)^2=\left(10x\right)^2-\left(x^2+25\right)^2=\left(10x-x^2-25\right)\left(10x+x^2+25\right)\)

\(=-\left(x-5\right)^2\left(x+5\right)^2\)

b) \(\left(x-y+5\right)^2-2\left(x-y+5\right)+1=\left(x-y+5-1\right)^2=\left(x-y+4\right)^2\)

c) \(\left(x^2+4y^2-5\right)^2-16\left(x^2+y^2+2xy+1\right)\)

Có lẽ bạn ghi sai đề rồi nha.

NH

Nguyễn Hải Ngọc

21 tháng 12 2017 - olm

phân tích đa thức thành nhân tử:

\(5\left(x-y\right)-y\left(x-y\right)\)

\(x^2-xy-8x+8y\)

\(x^2-10x+25-y^2\)

\(x^3-3x^2-4x+12\)

\(2x^2-2y^2-6x-6y\)

\(x^3-3x^2+3x-1\)

\(x^2+3x+2\)

#Hỏi cộng đồng OLM #Toán lớp 8

4

A

an

21 tháng 12 2017

A . 5(x-y)-y(x-y)

=(x6-y)(5-y)

B . x^2 - xy - 8x+8y

=(x^2-xy)-(8x-8y))

=x(x-y) - 8(x-y)

C. x^2-10x+25 - y^2

=(x^2 - 10x + 25 ) - y^2

=(x-5)^2 - y^2

=(x-5+y)(x-5-y)

D . x^3 - 3x^2-4x+12

=(x^3 - 3x^2 ) - (4x - 12)

=x^2 (x-3)-4(x-3)

=(x^2-4)(x-3)

=(x+2)(x-2)(x-3)

D . 2x^2-2y^2- 6x-6y

=(2^x - 2y^2) - (6x+ 6y)

=2(x^2 - y^2) - 6(x+y)

=2(x+y)(x-y) - 6(x+y)

=2(x+y)(x-y-3)

E . x^3 - 3x^2 + 3x - 1

=(x-1)^3

D.x^2+3x+2

=x^2+2x+x+2

=(x^2+2x)+(x+2)

=x(x+2)+(x+2)

=(x+2)(x+1)

NH

Nguyễn Hải Ngọc

21 tháng 12 2017

Sai vài chỗ nha bạn! :)

SG

Sách Giáo Khoa

21 tháng 4 2017

Làm tính cộng các phân thức sau :

a) \(\dfrac{5}{2x^2y}+\dfrac{3}{5xy^2}+\dfrac{x}{y^3}\)

b) \(\dfrac{x+1}{2x+6}+\dfrac{2x+3}{x\left(x+3\right)}\)

c) \(\dfrac{3x+5}{x^2-5x}+\dfrac{25-x}{25-5x}\)

d) \(x^2+\dfrac{x^4+1}{1-x^2}+1\)

e) \(\dfrac{4x^2-3x+17}{x^3-1}+\dfrac{2x-1}{x^2+x+1}+\dfrac{6}{1-x}\)

#Hỏi cộng đồng OLM #Toán lớp 8

6

AT

Anh Triêt

21 tháng 4 2017

Giải bài 25 trang 47 Toán 8 Tập 1 | Giải bài tập Toán 8

O

obito

16 tháng 6 2017

dap-an-bai-25_fix

L

LIÊN

2 tháng 10 2016

phân tích đa thức thành nhân tử

\(25\left(x-y\right)^20-16\left(x+y\right)^2\)

#Hỏi cộng đồng OLM #Toán lớp 8

2

LF

Lightning Farron

2 tháng 10 2016

25(x-y)²-16(x+y)²

=[5(x-y)]²-[4(x+y)]²

=[5x-5y]²-[4x+4y]²

=(5x-5y+4x+4y)[(5x-5y)-(4x+4y)]

=(9x-y)(x-9y)

L

LIÊN

2 tháng 10 2016

không có số 0 đâu nhá đánh lộn

K

©ⓢ丶κεη春╰‿╯

18 tháng 2 2020 - olm

B1 : a) làm tính nhân : \(\left(4x^3+3xy^2-2y^3\right)\left(3x^2-5xy-6y^2\right)\)b) phân tích đa thức thành nhân tử : \(8x^3+4x^2y-2xy^2-y^3\)\(4x^2y^2-4x^2-4xy-y^2\)c) tính GTBT :\(\left(5xy-4y^2\right)\left(3x^2+4xy\right)-15xy\left(x+y\right)\left(x-y\right)\)tại \(x=2,y=16\)d) thực hiện phép chia...

#Hỏi cộng đồng OLM #Toán lớp 8

3

GL

ღ๖ۣۜLinh's ๖ۣۜLinh'sღ] ★we are one★

18 tháng 2 2020

a, \(=12x^5+9x^3y^2-6x^2y^3-20x^4y-15x^2y^3-10xy^4-24x^3y^2-18xy^4+12y^5\)

(tự rút gọn cái :P)

b, \(8x^3+4x^2y-2xy^2-y^3\)

\(=4x^2\left(2x+y\right)-y^2\left(2x+y\right)=\left(2x+y\right)^2\left(2x-y\right)\)

\(4x^2y^2-4x^2-4xy-y^2=4x^2y^2-\left(2x+y\right)^2\)

\(=\left(2x+y+2xy\right)\left(2xy-2x+y\right)\)

Mấy cái còn lại nhân tung ra là được mà :))))

K

©ⓢ丶κεη春╰‿╯

21 tháng 2 2020

làm luôn đi cậu