Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Chu kì và tần số góc của con lắc.
Chu kì T = 1,2 s
Tần số góc là:
\(\omega=\dfrac{2\pi}{T}=\dfrac{2\pi}{1,2}=5,24\left(rad/s\right)\)
b) Vận tốc cực đại của vật.
Theo đồ thì biết biên độ A = 0,35
\(v_{max}=0,35\left(m/s\right)\)
c) Cơ năng của con lắc.
\(W=\dfrac{1}{2}mv_{max}^2=\dfrac{1}{2}\cdot0,2\cdot0,35^2=0,012\left(J\right)\)
d) Biên độ của vật.
\(A=\dfrac{v_{max}}{\omega}=\dfrac{0,35}{5,24}=0,067\left(m\right)\)

Biên độ: A=8
Pha ban đầu: pi
Chu kì: \(T=\dfrac{2pi}{4pi}=\dfrac{1}{2}\)
Tần số góc là 4pi

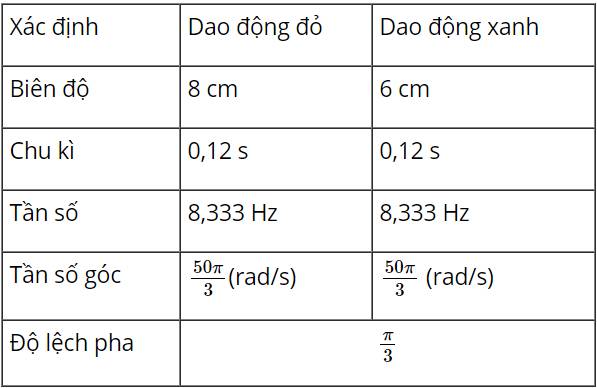
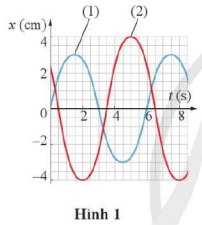
a) Dao động 1 (đường màu xanh) có:
- Biên độ: A1 = 3 cm
- Chu kì: T = 6 s
- Tần số: \(f=\dfrac{1}{T}=\dfrac{1}{6}\left(Hz\right)\)
Dao động 2 (đường màu đỏ) có:
- Biên độ: A2 = 4 cm
- Chu kì: T = 6 s
- Tần số: \(f=\dfrac{1}{T}=\dfrac{1}{6}\left(Hz\right)\)
b) Hai dao động có cùng chu kì nên \(\omega=\dfrac{2\pi}{T}=\dfrac{2\pi}{6}=\dfrac{\pi}{3}\left(rad/s\right)\)
Độ lệch thời gian của hai dao động khi cùng trạng thái: \(\Delta t=2,5s\)
Độ lệch pha: \(\Delta\varphi=\omega.\Delta t=\dfrac{\pi}{3}\cdot2,5=150^o\)
c) Tại thời điểm 3,5 s vật 2 đang ở VTCB nên vận tốc cực đại:
\(v=\omega A_2=\text{ }\dfrac{\pi}{3}\cdot4=\dfrac{4\pi}{3}\left(cm/s\right)\)
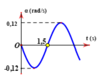
d) Tại thời điểm 1,5 s vật 1 đang ở biên dương nên gia tốc có giá trị:
\(a=-\omega^2A_1=-\dfrac{\pi^2}{9}\cdot3=-\dfrac{\pi^2}{3}\left(cm/s^2\right)\)
Độ lớn gia tốc khi đó là \(\dfrac{\pi^2}{3}cm/s^2\)
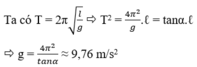
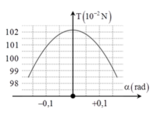
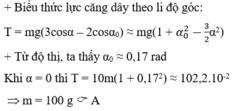

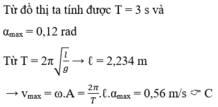


Vị trí của con lắc đơn được xác định bằng li độ dài s hay li độ góc α
Thế năng của con lắc đơn là thế năng trọng trường.
Chọn mốc tính thế năng ở vị trí cân bằng thì thế năng của con lắc ở li độ góc α là: Wt = mgl(1-cosα)
mà (1-cosα)=2\({\sin ^2}\frac{\alpha }{2}\) với α0 ≤ 10o thì\(\sin \frac{\alpha }{2} \approx \frac{\alpha }{2}\) (α tính theo rad)
Khi đó Wt = mgl\(\frac{{{\alpha ^2}}}{2}\) với α =\(\frac{s}{l}\) suy ra: Wt = mgl\(\frac{{{s^2}}}{{2{l^2}}}\)=\(\frac{1}{2}\)m\(\frac{g}{l}\)s2
Tại vị trí biên độ có Wt = W nên ta có \(\frac{1}{2}m\frac{g}{l}{s^2} = \frac{1}{2}m{\omega ^2}{A^2}\)
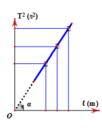
\( \to \omega = \sqrt {\frac{g}{l}} \to T = 2\pi \sqrt {\frac{l}{g}} \)
vậy với góc lệch α0 ≤ 10° thì chu kì của con lắc đơn gần như không phụ thuộc vào biên độ dao động