Question

[Hieu]

 làm cho mình câu đầu để làm mẫu mấy câu sau hihi

Answer 1

[Phong]

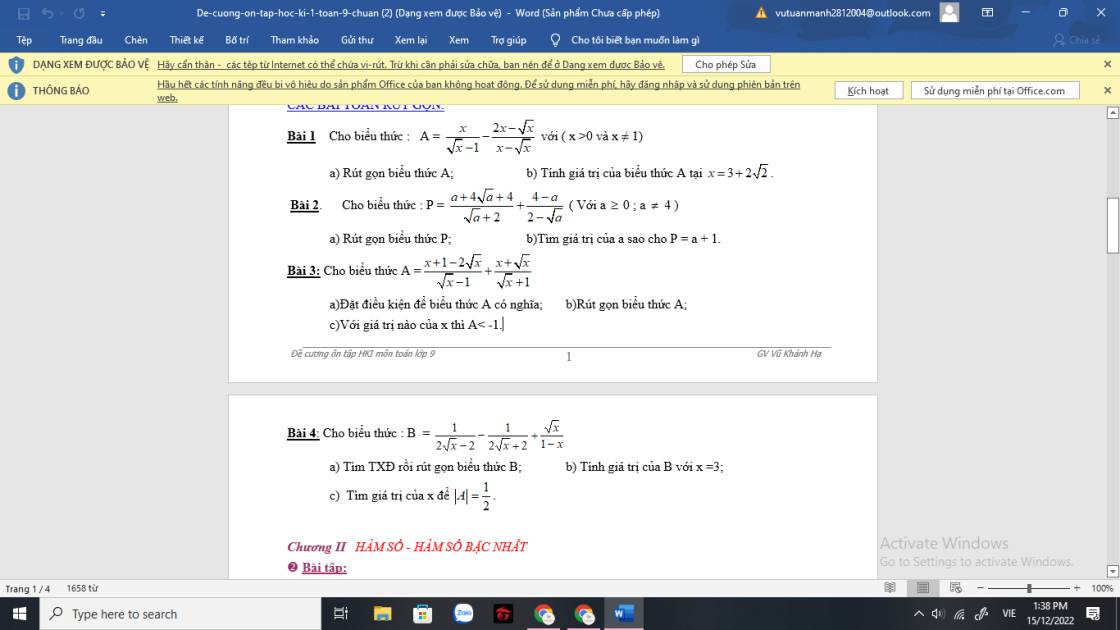
1) \(\sqrt{-2x+3}\) có nghĩa khi:

\(-2x+3\ge0\)

\(\Leftrightarrow-2x\ge-3\)

\(\Leftrightarrow2x\le3\)

\(\Leftrightarrow x\le\dfrac{3}{2}\)

2) \(\sqrt{-5x}\) có nghĩa khi:

\(-5x\ge0\)

\(\Leftrightarrow x\le0\)

3) \(\sqrt{\dfrac{x}{3}}\) có nghĩa khi:

\(\dfrac{x}{3}\ge0\)

\(\Leftrightarrow x\ge\dfrac{0}{3}\)

\(\Leftrightarrow x\ge0\)

4) \(\sqrt{1+x^2}\)

Mà: \(x^2\ge0\Rightarrow1+x^2\ge1>0\)

\(\sqrt{1-x^2}\) được xác định \(\forall x\)

5) \(\sqrt{\dfrac{4}{x+3}}\) có nghĩa khi:

\(\dfrac{4}{x+3}\ge0\) và \(x+3\ne0\)

Mà: \(4>0\)

\(\Leftrightarrow x+3>0\)

\(\Leftrightarrow x>-3\)

6) \(\sqrt{\dfrac{-5}{x^2+6}}\) 

Mà: \(-5< 0\)

\(x^2+6\ge6>0\forall x\)

\(\Rightarrow\dfrac{-5}{x^2+6}\le-\dfrac{5}{6}< 0\forall x\)

Biểu thức này không được xác định 

7) \(\sqrt{\dfrac{1}{-1+x}}\) có nghĩa khi: 

\(\dfrac{1}{x-1}\ge0;x-1\ne0\)

Mà: 1 > 0

\(\Leftrightarrow x-1>0\)

\(\Leftrightarrow x>1\)

8) \(\sqrt{\dfrac{2}{x^2}}\) có nghĩa khi:

\(\dfrac{2}{x^2}\ge0;x\ne0\)

\(\Leftrightarrow x\ne0\)

9) \(\sqrt{x^2-2x+1}\)

\(=\sqrt{\left(x-1\right)^2}\)

Mà: \(\left(x-1\right)^2\ge0\forall x\)

Biểu thức được xác định với mọi x 

10) \(\sqrt{-x^2-2x-1}\)

\(=\sqrt{-\left(x^2+2x+1\right)}\)

\(=\sqrt{-\left(x+1\right)^2}\)

Mà: \(\left(x+1\right)^2\ge0\forall x\)

\(\Rightarrow-\left(x+1\right)^2\le0\forall x\)

Nên biểu thức không được xác định 

Answer 2

[Phong]

11) \(\dfrac{1}{\sqrt{4x^2-12x+9}}=\dfrac{1}{\sqrt{\left(2x-3\right)^2}}=\dfrac{1}{\left|2x-3\right|}\)

Có nghĩa khi:

\(2x-3\ne0\)

\(\Leftrightarrow2x\ne3\)

\(\Leftrightarrow x\ne\dfrac{3}{2}\)

12) \(\sqrt{x^2-8x+15}\)

\(=\sqrt{x^2-8x+16+1}\)

\(=\sqrt{\left(x-4\right)^2+1}\)

Mà: \(\left(x-4\right)^2+1\ge1>0\forall x\)

Biểu thức được xác định với mọi x 

13) \(\sqrt{x-2}+\dfrac{1}{x-5}\) xác định khi:

\(\left\{{}\begin{matrix}x-2\ge0\\x-5\ne0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x\ge2\\x\ne5\end{matrix}\right.\)

14) \(\sqrt{\dfrac{2+x}{5-x}}\) có nghĩa khi: 

\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}2+x\ge0\\5-x>0\end{matrix}\right.\\\left\{{}\begin{matrix}2+x\le0\\5-x< 0\end{matrix}\right.\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x\ge-2\\x< 5\end{matrix}\right.\\\left\{{}\begin{matrix}x\le-2\\x>5\end{matrix}\right.\end{matrix}\right.\)

\(\Leftrightarrow-2\le x< 5\)

15) \(\sqrt{\dfrac{x-1}{x+2}}\)

\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x-1\ge0\\x+2>0\end{matrix}\right.\\\left\{{}\begin{matrix}x-1\le0\\x+2< 0\end{matrix}\right.\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x\ge1\\x>-2\end{matrix}\right.\\\left\{{}\begin{matrix}x\le1\\x< -2\end{matrix}\right.\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x\ge1\\x>-2\end{matrix}\right.\)