Khử mẫu của biểu thức lấy căn 3 2...

Khách

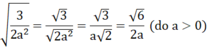
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

Pham Trong Bach

30 tháng 10 2018

Khử mẫu của biểu thức lấy căn 3 2 a 2 v ớ i a > 0

#Hỏi cộng đồng OLM #Toán lớp 9

Cao Minh Tâm

30 tháng 10 2018

Đúng(0)

Các câu hỏi dưới đây có thể giống với câu hỏi trên

Phạm Hà My

18 tháng 9 2020

khử mẫu của biểu thức lấy căn

\(\frac{x}{y}\) \(\sqrt{\frac{y}{x}}\) với x,y>0

2/ \(\sqrt{\frac{x}{64y^3}}\) với x,y>0

#Hỏi cộng đồng OLM #Toán lớp 9

yến phạm

30 tháng 7 2019

Khử mẫu của biểu thức lấy căn

\(\sqrt{\frac{\left(1+\sqrt{2}\right)^3}{27}}\)

Đưa 1 thừa số vào trong dấu căn

\(ab\sqrt{\frac{1}{a}+\frac{1}{b}}vớia>0,b>0\)

#Hỏi cộng đồng OLM #Toán lớp 9

Akai Haruma

Giáo viên

7 tháng 10 2020

Lời giải:

\(\sqrt{\frac{(1+\sqrt{2})^3}{27}}=\sqrt{\frac{(1+\sqrt{2})^3}{3^3}}=\sqrt{\frac{3(1+\sqrt{2})^3}{3^4}}\)

\(=\frac{(1+\sqrt{2})\sqrt{3+3\sqrt{2}}}{9}\)

\(ab\sqrt{\frac{1}{a}+\frac{1}{b}}=\sqrt{(ab)^2(\frac{1}{a}+\frac{1}{b})}=\sqrt{ab^2+a^2b}\)

Đúng(0)

Truong minh quan

13 tháng 7 2018 - olm

Khử mẫu của biểu thức lấy căn

1)√(a/b^2+a/b^4)

2)√a/4 với a>=0

3)√2a/8b^3 với a/b>=0

4)√3/27a^2 với a>0

#Hỏi cộng đồng OLM #Toán lớp 9

Truong minh quan

13 tháng 7 2018 - olm

Khử mẫu của biểu thức lấy căn

1)√(a/b^2+a/b^4)

2)√a/4 với a>=0

3)√2a/8b^3 với a/b>=0

4)√3/27a^2 với a>0

#Hỏi cộng đồng OLM #Toán lớp 9

Ngọc Thư

3 tháng 7 2017

khử mẫu của biểu thức lấy căn

a.\(\sqrt{\dfrac{4}{5}}\)

b.\(\sqrt{\dfrac{3}{125}}\)

c.\(\sqrt{\dfrac{3}{2a^3}}\) với a>0

#Hỏi cộng đồng OLM #Toán lớp 9

Nguyễn Thanh Danh

28 tháng 11 2017

a. 2√5

Đúng(0)

Nguyễn Vân

25 tháng 8 2017

Bài 1: Khử mẫu của biểu thức lấy căn: a) \(xy\sqrt{\dfrac{x}{y}}\) b) \(\sqrt{\dfrac{5a^3}{49b}}\left(a\ge0,b>0\right)\) Bài 2:Trục căn thức ở mẫu: a) \(\dfrac{\sqrt{3}-3}{1-\sqrt{3}}\) b) \(\dfrac{5-\sqrt{15}}{\sqrt{3}-\sqrt{5}}\) c) \(\dfrac{2\sqrt{2}+2}{5\sqrt{2}}\) ...

Đọc tiếp

#Hỏi cộng đồng OLM #Toán lớp 9

Mysterious Person

26 tháng 8 2017

bài 1) a) \(xy\sqrt{\dfrac{x}{y}}=x\sqrt{y}\sqrt{y}\dfrac{\sqrt{x}}{\sqrt{y}}=x\sqrt{x}\sqrt{y}=\left(\sqrt{x}\right)^3\sqrt{y}\)

b) \(\sqrt{\dfrac{5a^3}{49b}}=\dfrac{\sqrt{5a^3}}{\sqrt{49b}}=\dfrac{\sqrt{5a^3}}{7\sqrt{b}}=\dfrac{\sqrt{5a^3}.\sqrt{b}}{7\sqrt{b}.\sqrt{b}}=\dfrac{\sqrt{5a^3b}}{7b}\)

bài 2) a) \(\dfrac{\sqrt{3}-3}{1-\sqrt{3}}=\dfrac{\sqrt{3}\left(1-\sqrt{3}\right)}{1-\sqrt{3}}=\sqrt{3}\)

b) \(\dfrac{5-\sqrt{15}}{\sqrt{3}-\sqrt{5}}=\dfrac{-\sqrt{5}\left(\sqrt{3}-\sqrt{5}\right)}{\sqrt{3}-\sqrt{5}}=-\sqrt{5}\)

c) \(\dfrac{2\sqrt{2}+2}{5\sqrt{2}}=\dfrac{\sqrt{2}\left(2+\sqrt{2}\right)}{5\sqrt{2}}=\dfrac{2+\sqrt{2}}{5}\)

Đúng(0)

nguyễn hà quyên

16 tháng 9 2017 - olm

Khử mẫu của biểu thức lấy căn

a)\(\sqrt{\frac{2}{3}}\) b)\(\sqrt{\frac{x^2}{2}\left(x\ge0\right)}\) c)\(\sqrt{\frac{x}{y}}\left(x\ne0;y>0\right)\) d)\(\sqrt{\frac{9x^3}{25y}}\left(x>0;y>0\right)\)

#Hỏi cộng đồng OLM #Toán lớp 9

lưu hoàng hiệp

16 tháng 9 2017

mình mới học lớp 6 nên không biết

Đúng(0)

lưu hoàng hiệp

16 tháng 9 2017

mày xem sẽ chưa tao xem rồi đó về mà xem

Đúng(0)

Hải Dương

6 tháng 7 2019

Bài 1: khử mẫu của biểu thức lấy căn

1) \(\sqrt{\frac{2}{3-\sqrt{5}}}\)

2) \(\sqrt{\frac{a-4}{2\left(\sqrt{a}-2\right)}}\) (a > 4)

3) \(\sqrt{\frac{1}{a\left(1-\sqrt{3}\right)}}\)

4) \(\sqrt{\frac{a}{4-2\sqrt{3}}}\)

#Hỏi cộng đồng OLM #Toán lớp 9

tthnew

6 tháng 7 2019

EM thử thôi, ko chắc đâu ạ:( Sai thì xin thông cảm cho ạ.

1) \(\sqrt{\frac{2}{3-\sqrt{5}}}=\sqrt{\frac{2\left(3+\sqrt{5}\right)}{\left(3-\sqrt{5}\right)\left(3+\sqrt{5}\right)}}=\sqrt{\frac{6+2\sqrt{5}}{4}}=\frac{\sqrt{6+2\sqrt{5}}}{2}\)

2) \(\sqrt{\frac{a-4}{2\left(\sqrt{a}-2\right)}}=\sqrt{\frac{\left(a-4\right)\left(\sqrt{a}+2\right)}{2\left(\sqrt{a}-2\right)\left(\sqrt{a}+2\right)}}\)

\(=\sqrt{\frac{\left(a-4\right)\left(\sqrt{a}+2\right)}{2\left(a-4\right)}}\)

3) \(\sqrt{\frac{1}{a\left(1-\sqrt{3}\right)}}=\sqrt{\frac{1+\sqrt{3}}{a\left(1-\sqrt{3}\right)\left(1+\sqrt{3}\right)}}=\sqrt{\frac{1+\sqrt{3}}{a\left(1-3\right)}}=\sqrt{-\frac{1+\sqrt{3}}{2a}}\)

4) \(\sqrt{\frac{a}{4-2\sqrt{3}}}=\sqrt{\frac{a\left(4+2\sqrt{3}\right)}{\left(4-2\sqrt{3}\right)\left(4+2\sqrt{3}\right)}}=\sqrt{\frac{4a+2a\sqrt{3}}{16-12}}=\sqrt{\frac{4a+2a\sqrt{3}}{4}}=\frac{\sqrt{4a+2a\sqrt{3}}}{2}\)

Đúng(0)