Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.
a.\(\Delta=\left(4m+1\right)^2-8\left(m-4\right)=16m^2+33>0\left(\forall m\in R\right)\)
b.Gia su 2 nghiem cua PT la \(x_1,x_2\left(x_1>x_2\right)\)
Theo de bai ta co;\(x_1-x_2=17\)
Tu cau a ta co:\(x_1=\frac{-4m-1+\sqrt{16m^2+33}}{2}\) \(x_2=\frac{-4m-1-\sqrt{16m^2+33}}{2}\)
\(\Rightarrow\frac{-4m-1+\sqrt{16m^2+33}}{2}-\frac{-4m-1-\sqrt{16m^2+33}}{2}=17\)
\(\Leftrightarrow\frac{2\sqrt{16m^2+33}}{2}=17\)
\(\Leftrightarrow16m^2+33=289\)
\(\Leftrightarrow m=4\)
2.
a.\(\Delta'=\left(m-1\right)^2-\left(m+2\right)\left(3-m\right)=2m^2-3m-5=\left(m+1\right)\left(2m-5\right)>0\)
TH1:\(\hept{\begin{cases}m+1>0\\2m-5>0\end{cases}\Leftrightarrow m>\frac{5}{2}}\)
TH2:\(\hept{\begin{cases}m+1< 0\\2m-5< 0\end{cases}\Leftrightarrow m< -1}\)
Xet TH1:\(x_1=\frac{-m+1+\sqrt{2m^2-3m-5}}{m+2}\) \(x_2=\frac{-m+1-\sqrt{2m^2-3m-5}}{m+2}\)
Ta co:\(x^2_1+x^2_2=x_1+x_2\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1.x_2=x_1+x_2\)
\(\Leftrightarrow\left(\frac{-2m+2}{m+2}\right)^2-\frac{-m^2+5m+6}{\left(m+2\right)^2}=\frac{-2m+2}{m+2}\)
\(\Leftrightarrow\frac{5m^2-13m-2}{\left(m+2\right)^2}=\frac{-2m^2-2m+4}{\left(m+2\right)^2}\)
\(\Rightarrow7m^2-11m-6=0\)
\(\Delta_m=121+168=289>0\)
\(\Rightarrow\hept{\begin{cases}m_1=2\left(l\right)\\m_2=-\frac{3}{7}\left(l\right)\end{cases}}\)
TH2;Tuong tu
Vay khong co gia tri nao cua m de PT co 2 nghiem thoa man \(x^2_1+x^2_2=x_1+x_2\)

Ta có: \(x^2-5x+3=0\)
Áp dụng định lí viet ta có: \(\hept{\begin{cases}x_1+x_2=5\\x_1x_2=3\end{cases}}\)
a) \(A=x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2=5^2-2.3=19\)
b) \(B=x_1^3+x_2^3=\left(x_1+x_2\right)^3-3\left(x_1+x_2\right)x_1x_2=5^3-3.5.3=80\)
c) \(C=\left|x_1-x_2\right|\)>0
=> \(C^2=x_1^2+x_2^2-2x_1x_2=19-2.3=13\)
=> C = căn 13
d) \(D=x_2+\frac{1}{x_1}+x_1+\frac{1}{x_2}=\left(x_1+x_2\right)+\frac{x_1+x_2}{x_1x_2}=5+\frac{5}{3}=5\frac{5}{3}\)
e) \(E=\frac{1}{x_1+3}+\frac{1}{x_2+3}=\frac{\left(x_1+x_2\right)+6}{x_1x_2+3\left(x_1+x_2\right)+9}=\frac{5+6}{3+3.5+9}=\frac{11}{27}\)
g) \(G=\frac{x_1-3}{x_1^2}+\frac{x_2-3}{x_2^2}=\left(\frac{1}{x_1}+\frac{1}{x_2}\right)-3\left(\frac{1}{x_1^2}+\frac{1}{x_2^2}\right)\)
\(=\frac{x_1+x_2}{x_1x_2}-3\frac{x_1^2+x_2^2}{x_1^2.x_2^2}=\frac{5}{3}-3.\frac{19}{3^2}=-\frac{14}{3}\)

a) Thay m=1 vào phương trình ta được:
x2+2.1.x-6.1-9=0
<=> x2+2x-6-9=0
<=> x2+2x-15=0
<=> x2+5x-3x-15=0
<=> x(x+5)-3(x+5)=0
<=> (x-3)(x+5)=0
\(\Leftrightarrow\orbr{\begin{cases}x-3=0\\x+5=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=3\\x=-5\end{cases}}}\)
b) Thay x=2 vào phương trình ta được:
22+2.2.m-6m-9=0
<=> 4+4m-6m-9=0
<=> -2x-5=0
<=> -2x=5
<=> \(x=\frac{-5}{2}\)

\(\left(-5\right)^2-4.\left(-3\right)\left(-2\right)=25-24=1>0\)
Suy ra pt luôn có 2 nghiệm phân biệt
Theo Vi-ét:\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-5}{3}\\x_1x_2=\dfrac{2}{3}\end{matrix}\right.\)
\(M=x_1+\dfrac{1}{x_1}+\dfrac{1}{x_2}+x_2\\ =\left(x_1+x_2\right)+\dfrac{x_1+x_2}{x_1x_2}\\ =\dfrac{-5}{3}+\dfrac{-5}{3}:\dfrac{2}{3}\\ =\dfrac{-5}{3}-\dfrac{5}{2}\\ =\dfrac{-25}{6}\)
-3x2-5x-2=0
Ta có :-3-(-5)-2=0
=>Phương trình có 2 nghiệm \(\hept{\begin{cases}x_1=-1\\x_2=\frac{-5}{3}\end{cases}}\)
Thay x1;x2 vào M ta được:
M=(-1)+\(\frac{1}{-1}\)+\(\frac{1}{\frac{-5}{3}}\)+\(\frac{-5}{3}\)
=(-1)+(-1)+\(-\frac{3}{5}+-\frac{5}{3}\)
=\(-\frac{64}{15}\)

a) phương trình (1) có a=m-1 b'=b/2 = -m-1 c=m
\(\Delta=b'^2-ac=\left(-m-1\right)^2-\left(m-1\right)\cdot m\)
\(=m^2+2m+1-m^2+m=3m+1\)
Phương trình có hai nghiệm <=> \(\Delta\ge0\Leftrightarrow3m+1\ge0\Leftrightarrow m\ge-\frac{1}{3}\)
b) Khi phương trình có hai nghiệm x1, x2, theo hệ thức Vi-ét ta có
\(\hept{\begin{cases}x_1+x_2=\frac{2m+2}{m-1}=2+\frac{4}{m-1}\\x_1\cdot x_2=\frac{m}{m-1}=1+\frac{1}{m-1}\end{cases}}\)
\(\Rightarrow x_1+x_2-4x_1\cdot x_2=-2\)

Mình nghĩ với pt tổng quát: \(ax^2+bx+c=0\) có \(\Delta=b^2-4ac\)
Nếu như vậy thì: \(1.x^2+6x+m\) có \(\Delta=6^2-4m\)chứ?
Riêng mình thì bài này mình dùng delta phẩy cho lẹ:
Lời giải
Để pt \(x^2+6x+m=0\) có 2 nghiệm phân biệt thì:
\(\Delta'=\left(\frac{b}{2}\right)^2-ac=3^2-m>0\)
\(\Leftrightarrow m< 9\)
Đáp án C
Phương trình x 2 - 6x + 7 = 0 có △ = - 6 x 2 - 4.1.7 = 8 > 0 nên phương trình có hai nghiệm x 1 ; x 2
Theo hệ thức Vi-ét ta có: x 1 + x 2 =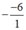 = 6
⇔
x
1
+
x
2
= 6
= 6
⇔
x
1
+
x
2
= 6