
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



11.
\(SA\perp\left(ABCD\right)\Rightarrow\) AC là hình chiếu vuông góc của SC lên (ABCD)
\(\Rightarrow\widehat{SCA}\) là góc giữa SC và (ABCD)
\(\Rightarrow\widehat{SCA}=\varphi\)
\(AC=BD=\sqrt{AB^2+AD^2}=a\sqrt{13}\)
\(tan\varphi=\frac{SA}{AC}=\frac{\sqrt{13}}{13}\)
12.
Hai vecto \(\overrightarrow{AB}\) và \(\overrightarrow{EF}\) song song cùng chiều
\(\Rightarrow\left(\overrightarrow{AB};\overrightarrow{EG}\right)=\left(\overrightarrow{EF};\overrightarrow{EG}\right)=\widehat{GEF}=45^0\)
8.
Qua O có 1 và chỉ 1 mặt phẳng vuông góc \(\Delta\)
9.
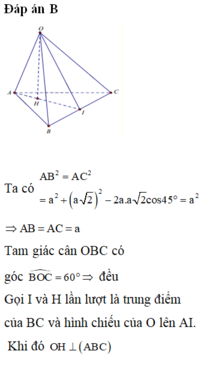
Gọi O là tâm tam giác BCD
\(\Rightarrow AO\perp\left(BCD\right)\Rightarrow AO\perp CD\)
Mà \(CD\perp BO\) (trung tuyến đồng thời là đường cao)
\(\Rightarrow CD\perp\left(ABO\right)\Rightarrow CD\perp AB\)
\(\Rightarrow\overrightarrow{AB}.\overrightarrow{CD}=0\)
10.
\(AB\perp AD\Rightarrow\widehat{BAD}=90^0\)

c/
\(\Leftrightarrow tan\left(60^0-x\right)=-\frac{1}{\sqrt{3}}\)
\(\Rightarrow60^0-x=-30^0+k180^0\)
\(\Rightarrow x=90^0+k180^0\)
d/
\(\Leftrightarrow tan\left(3x+\frac{2\pi}{5}\right)=-tan\left(\frac{\pi}{5}\right)\)
\(\Leftrightarrow tan\left(3x+\frac{2\pi}{5}\right)=tan\left(-\frac{\pi}{5}\right)\)
\(\Rightarrow3x+\frac{2\pi}{5}=-\frac{\pi}{5}+k\pi\)
\(\Rightarrow x=-\frac{\pi}{5}+\frac{k\pi}{3}\)
a/
\(\Leftrightarrow tan2x=-tan40^0\)
\(\Leftrightarrow tan2x=tan\left(-40^0\right)\)
\(\Rightarrow2x=-40^0+k180^0\)
\(\Rightarrow x=-20^0+k90^0\)
b/
\(\Leftrightarrow tan\left(2x-15^0\right)=1\)
\(\Rightarrow2x-15^0=45^0+k180^0\)
\(\Rightarrow x=30^0+k90^0\)

\(2sin\left(x-30^0\right)=\sqrt{2}\)
\(\Leftrightarrow sin\left(x-30^0\right)=\frac{\sqrt{2}}{2}=sin\left(45^0\right)\)
\(\Rightarrow\left[{}\begin{matrix}x-30^0=45^0+k360^0\\x-30^0=135^0+k360^0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=75^0+k360^0\\x=165^0+k360^0\end{matrix}\right.\)
\(sin2x=sin\left(x-\frac{2\pi}{3}\right)\)
\(\Rightarrow\left[{}\begin{matrix}2x=x-\frac{2\pi}{3}+k2\pi\\2x=\pi-x+\frac{2\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-\frac{2\pi}{3}+k2\pi\\x=\frac{5\pi}{9}+\frac{k2\pi}{3}\end{matrix}\right.\)
\(cos2x=sin\left(x-45^0\right)\)
\(\Leftrightarrow cos2x=cos\left(135^0-x\right)\)
\(\Rightarrow\left[{}\begin{matrix}2x=135^0-x+k360^0\\2x=x-135^0+k360^0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=45^0+k120^0\\x=-135^0+k360^0\end{matrix}\right.\)

\(cos3x=-cos\left(x-120^0\right)\)
\(\Leftrightarrow cos3x=cos\left(x+60^0\right)\)
\(\Rightarrow\left[{}\begin{matrix}3x=x+60^0+k360^0\\3x=-x-60^0+k360^0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=30^0+k180^0\\x=-15^0+k90^0\end{matrix}\right.\)
\(\Leftrightarrow sin\left(2x-90^0\right)=cos2x\)
\(\Leftrightarrow-cos2x=cos2x\)
\(\Rightarrow cos2x=0\Rightarrow2x=90^0+k180^0\)
\(\Rightarrow x=45^0+k90^0\)
\(cos^2x+sin^2x+2sinx.cosx=1+cos4x\)
\(\Leftrightarrow1+sin2x=1+cos4x\)
\(\Leftrightarrow cos4x=sin2x=cos\left(\frac{\pi}{2}-2x\right)\)
\(\Rightarrow\left[{}\begin{matrix}4x=\frac{\pi}{2}-2x+k2\pi\\4x=2x-\frac{\pi}{2}+k2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{12}+\frac{k\pi}{3}\\x=-\frac{\pi}{4}+k\pi\end{matrix}\right.\)

Câu 8:
Kẻ \(AH\perp SM\)
Trong mặt phẳng (SBC), qua H kẻ đường thẳng song song BC cắt SB và SC lần lượt tại P và Q
\(\Rightarrow\Delta APQ\) là thiết diện của (P) và chóp
\(AM=\frac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều)
\(\Rightarrow SA=AM\Rightarrow\Delta SAM\) vuông cân tại A
\(\Rightarrow AH=\frac{SA\sqrt{2}}{2}=\frac{a\sqrt{6}}{4}\) đồng thời H là trung điểm SM
\(\Rightarrow PQ=\frac{1}{2}BC=\frac{a}{2}\) (đường trung bình)
\(\Rightarrow S_{\Delta APQ}=\frac{1}{2}AH.PQ=\frac{a^2\sqrt{6}}{16}\)
Câu 9.
\(SH\perp\left(ABC\right)\Rightarrow\widehat{SAH}\) là góc giữa SA và (ABC)
\(SH=AH=\frac{a\sqrt{3}}{2}\Rightarrow\Delta SAH\) vuông cân tại H
\(\Rightarrow\widehat{SAH}=45^0\)
Câu 6:
Bạn kiểm tra lại đề, \(SO\perp\left(ABCD\right)\Rightarrow SO\perp OB\Rightarrow\widehat{SOB}=90^0\)
Nên không thể có chuyện \(tan\widehat{SOB}=\frac{1}{2}\)
Câu 7:
H là trực tâm tam giác ABC \(\Rightarrow BH\perp AC\)
Mà \(SA\perp\left(ABC\right)\Rightarrow SA\perp BH\)
\(\Rightarrow BH\perp\left(SAC\right)\Rightarrow BH\perp SC\) (1)
K là trực tâm tam giác SBC \(\Rightarrow BK\perp SC\) (2)
(1);(2) \(\Rightarrow SC\perp\left(BHK\right)\Rightarrow\) góc giữa SC và (BHK) bằng 90 độ

1. T= \(\frac{\pi}{\left|a\right|}=\frac{\pi}{3}\)
2. \(T_1=\frac{2\pi}{2}=\pi\) ; \(T_2=\frac{2\pi}{\frac{1}{2}}=4\pi\)
=> \(T=BCNN\left(\pi;4\pi\right)=4\pi\)
3. \(\left[{}\begin{matrix}5x-45^o=30^o+k360^o\\5x-45^o=-30^o+k360^o\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}5x=75^o+k360^o\\5x=15^o+k360^o\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=15^o+k72^o\\x=3^0+k72^o\end{matrix}\right.\) \(\left(k\in Z\right)\)
Cho k=-1 thì x= -57 độ or x= -69 độ nên lấy x= -57 độ là no âm lớn nhất => Chọn C
4. Có pt hoành độ giao điểm của 2 đths : sinx = sin3x
\(\Leftrightarrow\left[{}\begin{matrix}3x=x+k2\pi\\3x=\pi-x+k2\pi\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=k\pi\\x=\frac{\pi}{4}+\frac{k\pi}{2}\end{matrix}\right.\left(k\in Z\right)\)
trong \(\left(\frac{-\pi}{2};\frac{3\pi}{2}\right)\) với \(x=k\pi\Rightarrow k\in\left\{0;1\right\}\)
với \(x=\frac{\pi}{4}+\frac{k\pi}{4}\Rightarrow k\in\left\{-1;0;1;2\right\}\)
Vậy 2 đths cắt nhau tại 6 điểm trong \(\left(\frac{-\pi}{2};\frac{3\pi}{2}\right)\)
5. cot = \(\sqrt{3}\) \(\Leftrightarrow tanx=\frac{1}{\sqrt{3}}\Leftrightarrow x=\frac{\pi}{6}+k\pi\left(k\in Z\right)\)
x \(\in\left[0;2017\pi\right]\Rightarrow k\in\left\{0;1;2;....;2015;2016\right\}\)
Vậy ptrinh có 2017 nghiệm.
CHÚC BẠN HỌC TỐT..!!

c/
\(\Leftrightarrow2sinx.cosx-2\sqrt{3}cos^2x=0\)
\(\Leftrightarrow2cosx\left(sinx-\sqrt{3}cosx\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=0\\sinx-\sqrt{3}cosx=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{2}+k\pi\\sinx=\sqrt{3}cosx\left(1\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow\frac{sinx}{cosx}=\sqrt{3}\Leftrightarrow tanx=\sqrt{3}\)
\(\Rightarrow x=\frac{\pi}{3}+k\pi\)
d/
\(\Leftrightarrow tan\left(3x-50^0\right)=-cot\left(x-30^0\right)\)
\(\Leftrightarrow tan\left(3x-50^0\right)=tan\left(x+60^0\right)\)
\(\Rightarrow3x-50^0=x+60^0+k180^0\)
\(\Rightarrow x=55^0+k90^0\)
a/
\(\Leftrightarrow sinx=2cosx\)
Nhận thấy \(cosx=0\) không phải nghiệm, pt tương đương:
\(\frac{sinx}{cosx}=2\Leftrightarrow tanx=2\)
\(\Leftrightarrow tanx=tana\) (với \(a\in\left(0;\frac{\pi}{2}\right)\) sao cho \(tana=2\))
\(\Rightarrow x=a+k\pi\)
b/
\(tan2x=cotx=tan\left(\frac{\pi}{2}-x\right)\)
\(\Leftrightarrow2x=\frac{\pi}{2}-x+k\pi\)
\(\Rightarrow x=\frac{\pi}{6}+\frac{k\pi}{3}\)

Phép uay ua tâm O?
Phương pháp để làm dạng này, lấy \(K\left(x_1;y_1\right),I\left(x_2;y_2\right)\in\left(d\right)\) =>\(K'\left(x_1';y_1'\right);I'\left(x_2';y_2'\right)\) là ảnh của K' qua phép quay tâm O góc uay alpha. Khi đó \(K',I'\in\left(d'\right)\)
Áp dụng biểu thức tọa độ:
\(\left\{{}\begin{matrix}x_1'=x_1\cos\alpha-y_1\sin\alpha\\y_1'=x_1\sin\alpha+y_1\cos\alpha\end{matrix}\right.\)
Giờ ta sẽ áp dụng vô bài
Lấy \(K\left(1;2\right)\in\left(d\right)\Rightarrow\left\{{}\begin{matrix}x_K'=1.\cos60^0-2.\sin60^0=\frac{\sqrt{3}}{2}-1\\y_K'=1.\sin60^0+2.\cos60=\frac{1}{2}+\sqrt{3}\end{matrix}\right.\)
\(\Rightarrow K'\left(\frac{\sqrt{3}}{2}-1;\frac{1}{2}+\sqrt{3}\right)\)
\(I\left(4;3\right)\in\left(d\right)\Rightarrow\left\{{}\begin{matrix}x_I'=4.\cos60^0-3\sin60^0=2\sqrt{3}-\frac{3}{2}\\y_I'=4\sin60^0+3\cos60^0=2+\frac{3\sqrt{3}}{2}\end{matrix}\right.\)
\(\Rightarrow I'\left(2\sqrt{3}-\frac{3}{2};2+\frac{3\sqrt{3}}{2}\right)\)
Bạn tự làm nốt nha, giờ chỉ cần viết phương trình đt (d') đi ua 2 điểm K' và I' thôi. Cách chứng minh công thức kia tui chưa biết chứng minh, bởi tui mới đọc sơ sơ dạng này :( Để bao giờ tìm hiểu thêm