Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nhìn đồ thị y = sinx ta thấy trong đoạn [-π ; π] các điểm nằm phía trên trục hoành của đồ thị y = sinx là các điểm có hoành độ thuộc khoảng (0 ; π). Từ đố, tất cả các khoảng giá trị của x để hàm số đó nhận giá trị dương là (0 + k2π ; π + k2π) hay (k2π ; π + k2π) trong đó k là một số nguyên tùy ý.

Bài 5. Cosx = ![]() là phương trình xác định hoành độ giao điểm của đường thẳng y =
là phương trình xác định hoành độ giao điểm của đường thẳng y = ![]() và đồ thị y = cosx.
và đồ thị y = cosx.
Từ đồ thị đã biết của hàm số y = cosx, ta suy ra x = ![]() , (k ∈ Z), ( chú ý tìm giao điểm của đường thẳng cới đồ thị trong đoạn [-π ; π] và thấy ngay rằng trong đoạn này chỉ có giao điểm ứng với
, (k ∈ Z), ( chú ý tìm giao điểm của đường thẳng cới đồ thị trong đoạn [-π ; π] và thấy ngay rằng trong đoạn này chỉ có giao điểm ứng với ![]() rồi sử dụng tính tuần hoàn để suy ra tất cả các giá trị của x là x =
rồi sử dụng tính tuần hoàn để suy ra tất cả các giá trị của x là x = ![]() , (k ∈ Z)).
, (k ∈ Z)).

Đồ thị hàm số y = sin x trên đoạn [-2π, 2π]
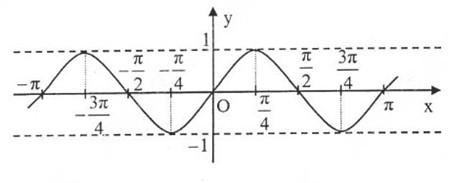
Dựa vào đồ thị hàm số y = sinx
a) Những giá trị của x ∈ [−3π2,2π][−3π2,2π] để hàm số y = sin x nhận giá trị bằng -1 là:
x=−π2;x=3π2x=−π2;x=3π2
b) Những giá trị của x ∈ [−3π2,2π][−3π2,2π] để hàm số y = sin x nhận giá trị âm là:
x ∈ (-π, 0) ∪ (π, 2 π)

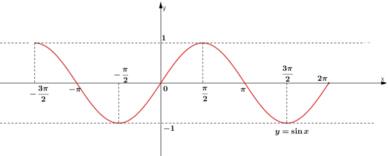
Đồ thị hàm số y = sin x:
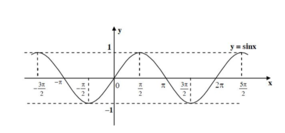
Dựa vào đồ thị hàm số y = sin x ta thấy
y = sin x > 0
⇔ x ∈ (-2π; -π) ∪ (0; π) ∪ (2π; 3π) ∪…
hay x ∈ (k2π; π + k2π) với k ∈ Z.

+ Vẽ đồ thị hàm số y = cos x.
+ Vẽ đường thẳng 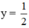
+ Xác định hoành độ các giao điểm.
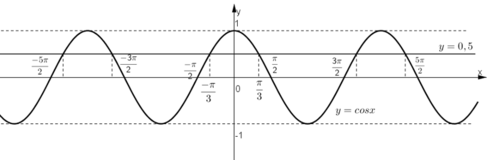
Ta thấy đường thẳng 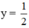 cắt đồ thị hàm số y = cos x tại các điểm có hoành độ
cắt đồ thị hàm số y = cos x tại các điểm có hoành độ


Xét đồ thị hàm số y = sin x trên 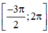 :
:
a. sin x = -1 ⇔ 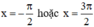
(Hoành độ giao điểm của đồ thị hàm số và đường thẳng y = -1).
b. sin x < 0
⇔ x ∈ (-π; 0) ∪ (π; 2π)
(Các khoảng mà đồ thị nằm phía dưới trục hoành).

Bài 1. a) trục hoành cắt đoạn đồ thị y = tanx (ứng với x ∈ ![]() ) tại ba điểm có hoành độ - π ; 0 ; π. Do đó trên đoạn
) tại ba điểm có hoành độ - π ; 0 ; π. Do đó trên đoạn ![]() chỉ có ba giá trị của x để hàm số y = tanx nhận giá trị bằng 0, đó là x = - π; x = 0 ; x = π.
chỉ có ba giá trị của x để hàm số y = tanx nhận giá trị bằng 0, đó là x = - π; x = 0 ; x = π.
b) Đường thẳng y = 1 cắt đoạn đồ thị y = tanx (ứng với x ∈ ![]() ) tại ba điểm có hoành độ
) tại ba điểm có hoành độ ![]() . Do đó trên đoạn
. Do đó trên đoạn ![]() chỉ có ba giá trị của x để hàm số y = tanx nhận giá trị bằng 1, đó là
chỉ có ba giá trị của x để hàm số y = tanx nhận giá trị bằng 1, đó là ![]() .
.
c) Phần phía trên trục hoành của đoạn đồ thị y = tanx (ứng với x ∈ ![]() ) gồm các điểm của đồ thị có hoành độ truộc một trong các khoảng
) gồm các điểm của đồ thị có hoành độ truộc một trong các khoảng ![]() . Vậy trên đoạn
. Vậy trên đoạn ![]() , các giá trị của x để hàm số y = tanx nhận giá trị dương là x ∈
, các giá trị của x để hàm số y = tanx nhận giá trị dương là x ∈ ![]() .
.
d) Phần phía dưới trục hoành của đoạn đồ thị y = tanx (ứng với x ∈ ![]() ) gồm các điểm của đồ thị có hoành độ thuộc một trong các khoảng
) gồm các điểm của đồ thị có hoành độ thuộc một trong các khoảng ![]() . Vậy trên đoạn
. Vậy trên đoạn ![]() , các giá trị của x để hàm số y = tanx nhận giá trị âm là x ∈
, các giá trị của x để hàm số y = tanx nhận giá trị âm là x ∈ ![]() .
.
a) \(\left\{-\pi;0;\pi\right\}\)
b) \(\left\{\dfrac{\pi}{4};\dfrac{\pi}{4}\pm\pi\right\}\)
c) \(\left(-\pi;-\dfrac{\pi}{2}\right)\cup\left(0;\dfrac{\pi}{2}\right)\cup\left(\pi;\dfrac{3\pi}{2}\right)\)
d) \(\left(-\dfrac{\pi}{2};0\right)\cup\left(\dfrac{\pi}{2};\pi\right)\)
Dựa vào đồ thị hàm số y = cosx, để làm số nhận giá trị âm thì:
x∈(−3π2;−π2);(π2;3π2)...⇒x∈(π2+k2π;3π2+k2π),k∈Zx∈(−3π2;−π2);(π2;3π2)...⇒x∈(π2+k2π;3π2+k2π),k∈Z