Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

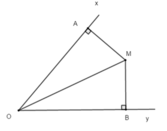
Gọi MA và MB theo thứ tự là khoảng cách từ M đến Ox và Oy
Xét hai tam giác vuông OMA và OMB có:
OM là cạnh chung
MA = MB (gt)
Do đó ΔOMA=ΔOMB (cạnh huyền – cạnh góc vuông)
Suy ra: M O A ^ = M O B ^ (hai góc tương ứng)
Vậy OM là tia phân giác của x O y ^
Vậy thứ tự sắp xếp phải là: b, c, a, d, e.
Chọn đáp án A

lấy độ dài cía thang trừ cho khoảng cách từ chân thang đến nhà (5-3)

5m 3m ?m A B C
- Áp dụng định lý pi - ta - go vào \(\Delta ABC\perp C\) ta được :
\(AB^2=AC^2+BC^2\)
Thay số : \(BC^2+3^2=5^2\)
=> \(BC=4\left(m\right)\)
Vậy khoảng cách từ mặt đất đến mái nhà là 4m .

Bài 1: Gọi chiều dài 3 tấm vải lúc đầu lần lượt là a,b,c.
Theo đề bài, ta có: a+b+c= 126 (m)
và \(a-\frac{1}{2}\cdot a=b-\frac{2}{3}\cdot b=c-\frac{3}{4}\cdot c\)
\(\Leftrightarrow\left(1-\frac{1}{2}\right)a=\left(1-\frac{2}{3}\right)b=\left(1-\frac{3}{4}\right)c\)
\(\Leftrightarrow\frac{1}{2}a=\frac{1}{3}b=\frac{1}{4}c\)
Áp dụng t/c của dãy tỉ số bằng nhau:
\(\frac{a}{2}=\frac{b}{3}=\frac{c}{4}=\frac{a+b+c}{2+3+4}=\frac{126}{9}=14\)
Đến đây tự tìm a,b,c.
Bài 2:
Gọi số sách ở 3 tủ lần lượt là a,b,c:
Theo đề bài, ta có: a+b+c = 2250
và \(\frac{a-100}{16}=\frac{b}{15}=\frac{c+100}{14}\)
Áp dụng t/c của dãy tỉ số bằng nhau:
\(\frac{a-100}{16}=\frac{b}{15}=\frac{c+100}{14}=\frac{a-100+b+c+100}{16+15+14}=\frac{2250}{45}=50\)
Tự tìm tiếp nha.
Bài 4: Gọi số hs khối 6,7,8,9 lần lượt là a.b.c.d .
Theo đề, ta có; b - d = 70
và \(\frac{a}{9}=\frac{b}{8}=\frac{c}{7}=\frac{d}{6}\)
Đặt \(\frac{a}{9}=\frac{b}{8}=\frac{c}{7}=\frac{d}{6}=k\)
\(\Rightarrow a=9k\)
\(b=8k\)
\(c=7k\)
\(d=6k\)
Thay b= 8k và d=6k vào b-d= 70:
8k - 6k = 70
2k = 70
k= 35
=> a=9k = 9* 35 = 315
(tìm b,c,d tương tự như tìm a. Sau đó kết luận)
Bài 5: Gọi số lãi của 2 tổ là a và b.
Theo đề , ta có: a+b = 12 800 000
và \(\frac{a}{b}=\frac{3}{5}\Rightarrow\frac{a}{3}=\frac{b}{5}\)
Áp dụng t/c của dãy tỉ số bằng nhau:
\(\frac{a}{3}=\frac{b}{5}=\frac{a+b}{3+5}=\frac{12800000}{8}=1600000\)
(tự tìm a,b)
Bài 6:
Gọi độ dài 3 cạnh của tam giác đó là a,b,c:
Theo đề, ta có: a+b+c=22
và \(\frac{a}{2}=\frac{b}{3}=\frac{c}{5}=\frac{a+b+c}{2+3+5}=\frac{22}{10}=2,2\)
=> (tự tìm a,b,c)
tỉ lệ khoảng cách giữa bản đồ và thực tế :
17/85=1:5
khoảng cách thực tế của ab :
12*5=60(km)
\(85\operatorname{km}=85\cdot10^5\left(\operatorname{cm}\right)\)
Tỉ lệ trên bản đồ là:
\(\frac{17}{85\cdot10^5}=\frac{1}{5\cdot10^5}\)
Khoảng cách thực tế giữa A và B là:
\(12:\frac{1}{5\cdot10^5}=12\cdot5\cdot10^5=60\cdot10^5\) (cm)=60(km)