K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
28 tháng 7 2017
Đáp án D.
* Phương pháp tự luận:
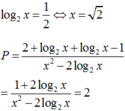
* Phương pháp trắc nghiệm: Thay x = 2 và biểu thức P = 2 .
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 5 2020
Lấy tích phân 2 vế:
\(\int\limits^1_0\left[f'\left(x\right)\right]^2dx+\int\limits^1_04\left(6x^2-1\right)f\left(x\right)dx=\int\limits^1_0\left(40x^6-44x^4+32x^2-4\right)dx=\frac{376}{105}\)
Xét \(I=\int\limits^1_0\left(6x^2-1\right)f\left(x\right)dx\)
Đặt \(\left\{{}\begin{matrix}u=f\left(x\right)\\dv=\left(6x^2-1\right)dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=f'\left(x\right)dx\\v=2x^3-x\end{matrix}\right.\)
\(\Rightarrow I=\left(2x^3-x\right)f\left(x\right)|^1_0-\int\limits^1_0\left(2x^3-x\right)f'\left(x\right)dx=1-\int\limits^1_0\left(2x^3-x\right)f'\left(x\right)dx\)
\(\Rightarrow\int\limits^1_0\left[f'\left(x\right)\right]^2dx+4-4\int\limits^1_0\left(2x^3-x\right)f'\left(x\right)dx=\frac{376}{105}\)
\(\Leftrightarrow\int\limits^1_0\left[f'\left(x\right)-2\left(2x^3-x\right)\right]^2dx-\int\limits^1_04\left(2x^3-x\right)^2dx=-\frac{44}{105}\)
\(\Leftrightarrow\int\limits^1_0\left[f'\left(x\right)-2\left(2x^3-x\right)\right]^2dx-\frac{44}{105}=-\frac{44}{105}\)
\(\Leftrightarrow\int\limits^1_0\left[f'\left(x\right)-\left(4x^3-2x\right)\right]^2dx=0\)
\(\Rightarrow f'\left(x\right)=4x^3-2x\Rightarrow f\left(x\right)=x^4-x^2+C\)
\(f\left(1\right)=1\Rightarrow1-1+C=1\Rightarrow C=1\)
\(\Rightarrow f\left(x\right)=x^4-x^2+1\)
\(\Rightarrow\int\limits^1_0x\left(x^4-x^2+1\right)dx=\frac{5}{12}\)
D
2 tháng 12 2021
*Đâu phải chia lúc nào cũng lớn hơn trừ đâu bạn,
VD: 10 : 5 = 1, Mà 10 - 5 = 5,
Vậy 10 : 5 < 10 - 5 (vì 1 < 5)
*Hay lấy ví dụ của bạn thì 10 : 9 = 1, (1) Mà 10 - 9 = 1
Vậy 10 : 9 > 10 - 9
*Cũng có trường hợp bằng nhau, ví dụ như: 4 : 2 = 2 Mà 4 - 2 = 2
Vậy 4 : 2 = 4 - 2
hoctot
12 tháng =1 năm