Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Số kết quả xảy ra khi chọn ngẫu nhiên 3 sản phẩm là: \(C_{20}^3\) ( kết quả )
b) Chọn ngẫu nhiên 3 sản phẩm từ 20 sản phẩm ta được một tổ hợp chập 3 của 20. Do đó, số phần tử của không gian mẫu là: \(n\left( \Omega \right) = C_{20}^3\)( phần tử)
Gọi A là biến cố “Cả 3 sản phẩm được chọn là chính phẩm”
Để chọn được cả 3 sản phẩm đều là chính phẩm thì ta phải chọn 3 sản phẩm từ 16 chính phẩm tức là ta được một tổ hợp chập 3 của 16 phần tử. Do đó số phần tử của biến cố A là: \(n\left( A \right) = C_{16}^3\)( phần tử)
Vậy xác suất của biến cố A là: \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{C_{16}^3}}{{C_{20}^3}} = \frac{{28}}{{57}}\).

Dễ thấy, X nhận các giá trị thuộc tập \(\left\{0;1;2\right\}\)
Xác suất để lấy ra 3 sản phẩm không có phế phẩm:
\(P\left(X=0\right)=\dfrac{C^0_2.C_4^{3-0}}{C^3_6}=\dfrac{1}{5}\)
Xác suất để lấy ra 2 sản phẩm không phế phẩm và 1 sản phẩm phế phẩm:
\(P\left(X=1\right)=\dfrac{C^1_2.C^{3-1}_4}{C^3_6}=\dfrac{3}{5}\)
Xác suất để lấy ra 1 sản phẩm không phế phẩm và 2 sản phẩm phế phẩm:
\(P\left(X=2\right)=\dfrac{C^2_2.C^{3-2}_4}{C^3_6}=\dfrac{1}{5}\)
bảng phân phối xác suất của X:
| X | P(X) |
| 0 | \(\dfrac{1}{5}\) |
| 1 | \(\dfrac{3}{5}\) |
| 2 | \(\dfrac{1}{5}\) |

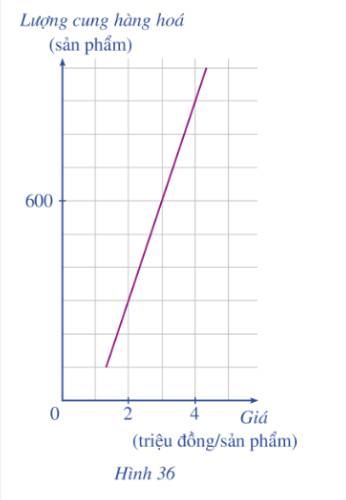
a) Từ đồ thị ta thấy khi giá bán là 2 triệu đồng/sản phẩm thì lượng cung hàng hóa là: 300 sản phẩm, khi giá bán là 4 triệu đồng/sản phẩm thì lượng cung hàng hóa là 900 sản phẩm.
b) Khi nhu cầu thị trường là 600 sản phẩm, để cân bằng thị trường thì lượng cung bằng lượng cầu. Khi đó lượng cung hàng hóa cũng là 600 sản phẩm.
Từ đồ thị ta thấy khi lượng cung hàng hóa là 600 sản phẩm thì giá bán là 3 triệu đồng/sản phẩm.

a) Thay x=100 ta được:
\(y = - {200.100^2} + 92000.100 - 8400000\)
\( = - 1200000\)
Thay x=200 ta được:
\(\begin{array}{l}y = - {200.200^2} + 92000.200 - 8400000\\ = 2000000\end{array}\)
Vậy với \(x = 100\) thì \(y = - 1200000\)
Với \(x = 200\) thì \(y = 2000000\)
b) Với mỗi giá trị của x có 1 giá trị tương ứng của y.

- Gọi số xe loại A và loại B cần dùng là x và y xe .
=> Số tiền là : \(T=4x+3y\)
Mà \(\left\{{}\begin{matrix}20x+10y\ge140\\0,6x+1,5y\ge9\end{matrix}\right.\) và \(\left\{{}\begin{matrix}x\ge0\\y\ge0\end{matrix}\right.\)
Ta có :

Gọi x là số đơn vị sản phẩm loại I, y là số đơn vị sản phẩm loại II được nhà máy lập kế hoạch sản xuất. Khi đó số lãi nhà máy nhân được là P = 3x + 5y (nghìn đồng).
Các đại lượng x, y phải thỏa mãn các điều kiện sau:
(I)
(II)
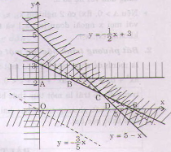
Miền nghiệm của hệ bất phương trình (II) là đa giác OABCD (kể cả biên).
Biểu thức F = 3x + 5y đạt giá trị lớn nhất khi (x; y) là tọa độ đỉnh C.
(Từ 3x + 5y = 0 => y = Các đường thẳng qua các đỉnh của OABCD và song song với đường y =
cát Oy tại điểm có tung độ lớn nhất là đường thẳng qua đỉnh C).
Phương trình hoành độ điểm C: 5 - x = <=> x = 4.
Suy ra tung độ điểm C là yc = 5 - 4 = 1. Tọa độ C(4; 1). Vậy trong các điều kiện cho phép của nhà máy, nếu sản xuất 4 đơn vị sản phẩm loại I và 1 đơn vị sản phẩm đơn vị loại II thì tổng số tiền lãi lớn nhất bằng:
Fc = 3.4 + 5.1 = 17 nghìn đồng.


Gọi p là tỉ lệ phế phẩm của kho hàng, với độ tin cậy \(\gamma\), khoảng tin cậy của p có dạng :
\(f_n-\frac{\sqrt{f_n\left(1-f_n\right)}}{\sqrt{n}}\Phi^{-1}\left(\frac{\gamma}{2}\right)< p< f_n+\frac{\sqrt{f_n\left(1-f_n\right)}}{\sqrt{n}}\Phi^{-1}\left(\frac{\gamma}{2}\right)\)(*)
Theo đề bài ta có: n= 400 \(\Rightarrow\sqrt{n}=20\)
\(f_n=\frac{20}{400}=0,05\); \(\gamma=0,95\Rightarrow\Phi^{-1}\left(\frac{\gamma}{2}\right)=\Phi^{-1}\left(0,475\right)=1,96\)
(*)\(\Leftrightarrow0,05-\frac{\sqrt{0,05.0,95}}{20}.1,96< p< 0,05+\frac{\sqrt{0,05.0,95}}{20}.1,96\)
\(\Leftrightarrow0,05-0,02< p< 0,05+0,02\)
\(\Leftrightarrow0,03< p< 0,07\)
Vậy khoảng tin cậy của tỉ lệ phế phẩm của kho hàng là : 0,03 < p < 0 ,07
thanks nha!!!!