MN
3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
30 tháng 4 2019
a) ∀ x ∈ R: x.1 = x
b) ∃ a ∈ R: a + a = 0
c) ∀ x ∈ R: x + (-x) = 0
N
3
1 tháng 2 2021
Có : \(P=4x+\dfrac{16}{x^2}=2x+2x+\dfrac{16}{x^2}\)
- AD AMGM : \(2x+2x+\dfrac{16}{x^2}\ge3\sqrt[3]{\dfrac{2x.2x.16}{x^2}}=12\)
- Dấu " = " xảy ra \(\Leftrightarrow2x=\dfrac{16}{x^2}\)
\(\Leftrightarrow2x^3=16\)
\(\Leftrightarrow x=2\) ( TM )
Vậy ....
( Chắc đề như vầy :vvv )
BT
18 tháng 5 2017
TenAnh1
TenAnh1
A = (-4.3, -5.94)
A = (-4.3, -5.94)
A = (-4.3, -5.94)
B = (11.06, -5.94)
B = (11.06, -5.94)
B = (11.06, -5.94)
D = (10.84, -5.94)
D = (10.84, -5.94)
D = (10.84, -5.94)
Số các véc tơ khác \(\overrightarrow{0}\) bằng véc tơ \(\overrightarrow{OC}\) có điểm đầu và điểm cuối là đỉnh lục giác là:
\(\overrightarrow{AB};\overrightarrow{BA};\overrightarrow{FO};\overrightarrow{OF};\overrightarrow{ED};\overrightarrow{DE};\overrightarrow{FC};\overrightarrow{CF}\).
Có 8 véc tơ.
CM
19 tháng 12 2019
Ta có d 2 : 3 x − 2 y + 1 = 0 ⇔ 6 x − 4 y + 2 = 0
Ta có điểm A(-1; 1) thuộc đường thẳng d2,.
Vì hai đường thẳng d1 và d2 song song với nhau nên ta có:
d ( d 1 ; d 2 ) = d ( A ; d 1 ) = 6. ( − 1 ) − 4. ( − 1 ) + 5 6 2 + ( − 4 ) 2 = 3 52
ĐÁP ÁN D
CM
17 tháng 6 2017
Ta có hệ số a= 5; b= 0 và c= -11 nên bán kính là R= a 2 + b 2 - c = 6
Chọn A.
CM
5 tháng 6 2019
Ta viết lại phương trình đường tròn: x2+ y2-2x + 3y -3= 0
Suy ra a= 1; b= -1,5 và c= -3 và bán kính R= 1 2 + 1 , 5 2 + 3 2 = 5 2
Chọn A.
16 tháng 5 2017
a) \(\forall x\in\mathbb{R}:x+\left(-x\right)=0\) (đúng)
Phủ định là \(\exists x\in\mathbb{R}:x+\left(-x\right)\ne0\) (sai)
b) \(\forall x\in\mathbb{R}\)\ \(\left\{0\right\}:x.\dfrac{1}{x}=1\) (đúng
Phủ định là \(\exists x\in\mathbb{R}\)\ \(\left\{0\right\}:x.\dfrac{1}{x}\ne1\) (sai)
c) \(\exists x\in R:x=-x\) (đúng)
Phủ định là \(\forall x\in\mathbb{R}:x\ne-x\) (sai)
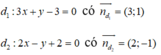
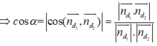
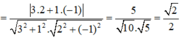
0
0