Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: SỐ cách xếp là;
5!*6!*2=172800(cách)
b: Số cách xếp là \(6!\cdot5!=86400\left(cách\right)\)

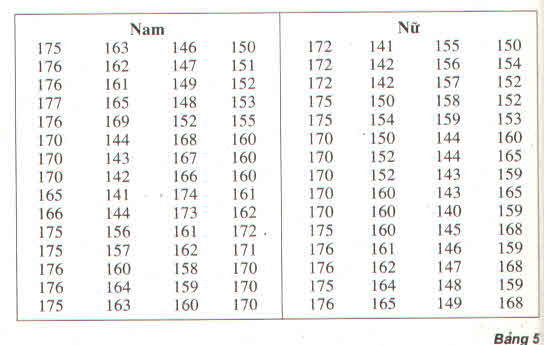
a) Dãy các số liệu chiều cao của các học sinh nam ở bảng 5 có :
\(\overline{x_1}\approx163\left(cm\right);s_1^2\approx134,3;s_1\approx11,59\)
Dãy các số liệu chiều cao của các học sinh nữ cho ở bảng 5 có :
\(\overline{x_2}\approx159,5\left(cm\right);s_2^2\approx148;s_2\approx12,17\)
b) Nhóm T có \(\overline{x_3}=163\left(cm\right);s_3^2=169;s_3=13\)
Học sinh ở nhóm nam và nhóm T có chiều cao như nhau và cùng lớn hơn chiều cao của học sinh ở nhóm nữ (vì \(\overline{x}_1=\overline{x}_3>\overline{x}_2\)
Vì \(\overline{x}_1=\overline{x}_3=163\left(cm\right)\) và \(s_1< s_3\) nên chiều cao của các học sinh nam đồng đều hơn chiều cao của các học sinh nhóm T

Không gian mẫu: \(12!\)
Xếp 8 nam: có \(8!\) cách
8 nam tạo thành 9 khe trống, xếp 4 nữ vào 9 khe trống này: \(A_9^4\) cách
\(\Rightarrow8!.A_9^4\) cách
Xác suất: \(P=\dfrac{8!.A_9^4}{12!}=\)
Câu này có thể coi như không giải theo cách gián tiếp được (thực ra là có giải được nhưng ko ai giải kiểu đó hết), nó bao gồm các trường hợp 4 nữ cạnh nhau, 3 nữ cạnh nhau, 2 nữ cạnh nhau, trong đó trường hợp trước còn bao hàm trường hợp sau cần loại trừ nữa

50% = 5/10 ; 2/5 = 4/10
số học sinh nữ là :
45 : (5 + 4) x 5 = 25 (học sinh)
đáp số : 25 học sinh
50%=1/2
Gọi số HS nam là a; số HS nữ là b
Ta có:2/5*a=1/2*b
=>a=1/2*b:2/5
a=1/2:2/5*b
a=5/4*b
Mà a+b=45
Hay 5/4*b+b=45
b*(5/4+1)=45
b*9/4=45
b=45:9/4
b=20(Vô lý vì a=25 mà 25/45=5/9 chứ ko phải là 4/9)
Còn b=25 thì a=20(cũng vô lý vì 50% của 25 thì là 12,5 không thuộc N)
Tui sửa lại đề:2/5 số HS nữ =50% số HS nam
Ta có :1/2*a=2/5*b
=> a=2/5:1/2*b
a=4/5*b
Mà a+b=45
Hay 4/5*b+b=45
b*(4/5+1)=45
b*9/5=45
b=45:9/5
b=25
Vậy số HS nữ của lớp 6a là 25 HS

Để 2 học sinh nam ko ngồi đối diện và ngồi cạnh nhau nên ta có 2 lựa chọn
Lựa chọn 1 : 7 bạn nam ngồi lần lượt vào các vị trí ghế 1,3,5,7,9 vá các bạn nữ ngồi 2,4,6,8,10,12,14
Khi đó: ghế số 1 có 7 lựa chon
ghế số 2 có 6 lựa chọn
ghế số 3 có 5 lựa chon
ghế số 4 có 4 lựa chon
ghế số 5 có 3 lựa chon
ghế số 6 có 2 lựa chon
ghế số 7 có 1 lựa chon
=> có 7x6x5x4x3x2x1 = 5040 cách xếp các bạn nam
Tương tự cũng sẽ có 5040 cách xếp các bạn nữ
Lựa chọn 2: Các bạn nam ngồi vào các ghế số 2,4,6,8,10,12,14
=> Tương tự ta cũng có 5040 cách xếp các bạn nam
và 5040 cách xếp các bạn nữ
Vậy qua 2 lựa chọn ta có 5040x4= 20160 cách xếp

Xếp 4 bạn nữ: có \(4!\) cách
4 bạn nữ tạo ra 5 khe trống, xếp 2 bạn nam vào 5 khe trống đó: \(A_5^2\) cách
Vậy tổng cộng có \(4!.A_5^2\) cách xếp thỏa mãn

Gọi số hs của 3 lớp lần lượt là a,b,c
Ta có :
\(a-\frac{1}{4}a=b-\frac{1}{7}b=c-\frac{1}{3}c\) và \(a+b+c=144\)
\(\Leftrightarrow\frac{3a}{4}=\frac{6b}{7}=\frac{2c}{3}\)
\(\Leftrightarrow\frac{a}{\frac{4}{3}}=\frac{b}{\frac{7}{6}}=\frac{c}{\frac{3}{2}}\)
Theo tính chất dãy tỉ số bằng nhau ta có :
\(\frac{a}{\frac{4}{3}}=\frac{b}{\frac{7}{6}}=\frac{c}{\frac{3}{2}}=\frac{a+b+c}{\frac{4}{3}+\frac{7}{6}+\frac{3}{2}}=\frac{144}{4}=36\)
\(\Leftrightarrow\left\{{}\begin{matrix}\frac{a}{\frac{4}{3}}=36\\\frac{b}{\frac{7}{6}}=36\\\frac{c}{\frac{3}{2}}=36\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=48\\b=42\\c=54\end{matrix}\right.\)
Vậy...

Chọn hai học sinh từ tổ sao cho 2 học sinh cùng giới có 2 công đoạn
\(CD_1:\) Chọn 1 bạn nữ trong 5 bạn nữ \(\Rightarrow\) Có 5 cách chọn
\(CD_2:\) Chọn 1 bạn nam trong 4 bạn nam \(\Rightarrow\) Có 4 cách chọn
Áp dụng quy tắc nhân, ta có : \(5.4=20\) ( cách chọn )
Vậy có 20 cách chọn 2 học sinh từ tổ để 1 bàn có 2 học sinh cùng giới
Lời giải:
Chọn 2 học sinh cùng giới tính nam, có: $C^2_4=6$ cách
Chọn 2 học sinh cùng giới tính nữ, có: $C^2_5=10$ cách
Tổng số cách chọn: $6+10=16$ (cách)